В плазме предполагаем сначала наличие частиц одного сорта. Вводим концентрацию частиц с номером 
в точке 
: 
.
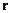- макроскопическое значение концентрации частиц.
Условие нейтральности означает:
В некотором окрестном объеме суммарный заряд близок к нулю, но нулю не равен:
Концентрация заряженных частиц в различных плазмах (космическая, лазерная, и др.) разная и колеблется очень существенно:
Часто накладывается ограничение: в плазме должно содержаться много частиц, чтобы проявлялись их коллективные свойства.
Используют формулу из статистической физики:
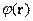- это электростатический потенциал.
Запишем уравнение Пуассона для электростатического потенциала в плазме:
Используем идею самосогласования для электростатического потенциала.
Рассмотрим точечный заряд 
в плазме, тогда 
. Запишем 
всей среды – в ней надо учесть и 
и плотность зарядов остальной среды. Тогда
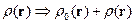
Используем формулу . В экспоненте стоит потенциал 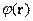, который и нужно найти. Для упрощения задачи разложим экспоненту в ряд. Если энергия электростатического взаимодействия во много раз меньше энергии теплового взаимодействия, т.е. плазма идеальная, то
при условии, что 
(тепловое взаимодействие много больше электростатического).
Условие идеальности плазмы принимает вид:
Тогда
Подставим в уравнение Пуассона:
,
где 
, 
- дебаевский радиус экранирования.
Мы получили уравнение Клейна, оно получается из уравнения Гельмгольца при замене 
. Решение уравнения Гельмгольца мы знаем:
- функция Грина
Тогда решение уравнения Клейна:
Часто пишут
т.е. кулоновский потенциал, умноженный на экспоненту (влияние плазмы).
На расстоянии 
от заряда потенциал убывает в е раз по сравнению с кулоновским и им пренебрегают. Потенциал экранируется зарядами противоположного знака из плазмы.
Для реализации коллективных свойств необходимо, чтобы концентрация частиц в объеме плазмы радиуса 
была много больше единицы, т.е. 
.
