Волновое уравнение для 
:
ð 
Где - это различные компоненты векторов 
.
Волна плоская, т.к. фронт распространения волны представляет собой плоскость.
Имеем систему координат, точку на фронте волны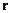 
,
нормаль к фронту волны 
. Тогда уравнение фронта волны (т.е. плоскости): 
. Но т.к. эта плоскость движется, то появляется зависимость от времени.
Если фронт волны- сфера, т.е. волна сферическая, то уравнение фронт а волны 
и:
Учтём обстоятельство, что форма фронта волны налагает на некоторые ограничения. Введём некоторые вспомогательные координаты:
И будем упрощать оператор ð 
. Можно перейти от (
) к (
). Рассчитаем 
и 
, где функция 
- сложная.
Рассмотрим компоненту: 
. Тогда:
Следовательно:
Это для случая плоской монохроматической волны. В результате имеем:
Тогда оператор ð 
Итак, ð 
, тогда 
.
где 
. Следовательно, 
Тогда 
, где 
и 
Выясним, как происходит движение фронтов волны для 1 и для 2 случаев:
1 случай:
, 
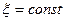
Получили, что фронт волны перемещается. Продифференцируем (*) по времени:
где 
- фазовая скорость. Тогда 
. Для среды 
, для вакуума 
, тогда 
. Для вакуума 
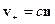
2 случай:
, 
Продифференцируем (**) по времени:
- фазовая скорость
И мы поучили, что фронт волны распространяется в обе стороны. Если волна не встречает препятствий, то решение - 
и 
, иначе решение усложняется.
