Уравнения Максвелла в случае квазистационарности:
Здесь учтено, что 
и 
.
На два последних уравнения Максвелла подействуем 
:
- уравнение квазистационарного поля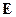 
Аналогично получаем для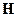 
:
Пусть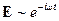 
; 
, тогда:
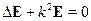
где 
Размерность 
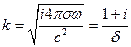
- параметр глубины проникновения поля 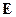. Мы получили уравнение Гельмгольца:
Вид решения для 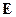зависит от формы области, где ищется решение. Если ищем в полупространстве, то 
- если взять 
тогда получим 
. Это даёт граничное условие 
Если взять 
, то это даст граничное условие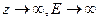 
, не объясняется ни физически, ни подтверждается экспериментально. Таким образом, следует брать 
-параметр: 
Для поля 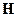аналогично:
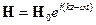- решение для полупространства.
Будем учитывать проникновение поле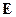й и 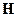только на глубину , т.к. дальше их проникновение мало, и его можно не учитывать, хотя оно существует.
