Уравнения Максвелла в среде:
Уравнения связи для однородной изотропной среды:
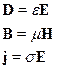
Будем рассматривать не магнитные материалы, т.е. 
.
Случай квазистационарных полей означает, что поля считаем в одних случаях стационарными, а в других случаях – не стационарными. Для квазистационарных полей:
1) 
, а 
отбрасываем, т.к.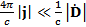 
2) 
- оставляем как есть.
Критерий применимости:
Если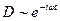 
, то 
. Слагаемое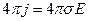 
. В гауссовой системе единиц 
имеет размерность как 
.
Составим отношение для сравниваемых слагаемых:
Это есть критерий или условие квазистационарности. И тогда:
Рассмотрим, как упрощается 
:
Запишем закон сохранения заряда в форме уравнения непрерывности:
, 
Используем (*), тогда:
, где 
Общее решение этого уравнения: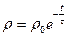 
Для сред с высокой проводимостью 
мала, 
, где 
- период, тогда:
Но поле может и не меняться по гармоническому закону, а может меняться как угодно, тогда - время, за которое поле меняется существенно.
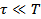
Тогда
, и 
Т.е. заряды быстро рассасываются. Значит для квазистационарного случая
В итоге получаем для квазистационарного случая систему уравнений Максвелла:
В квазистационарных полях есть эффекты:
1)Скин-эффект – быстропеременное поле вытесняется на поверхность проводника.
2)Токи Фуко – переменное магнитное поле создаёт электрические токи внутри проводника.
