по величине и по направлению постоянен в рассматриваемой области.
Запишем дипольный момент этого диэлектрика:
Здесь - константа.
Найдём потенциал, который создаёт однородно-поляризованный диэлектрик:
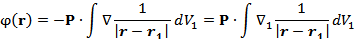
, где 
- интеграл-вектор:
Результат интегрирования зависит от формы поверхности.
Результат так же зависит от местонахождения точки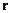 
(внутри объёма или вне объёма).
Для точки, принадлежащей объёму, например эллипсу:
, где 
- тензор, определяемый формой области, по которой производится интегрирование. - тензор деполяризации. Тензор для таких областей:
тогда 
. Для трехосного эллипсоида тензор можно представить в виде матрицы:
След этой матрицы 
.
Если область в виде шара, то все направления одинаковы, т.е. 
и тогда:
Если область – бесконечный цилиндр и если 
, тогда 
и им можно пренебречь. Тогда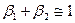 
. В круговом сечении (если цилиндр круговой), т.е. при 
: 
.
Примечание:
Пусть есть цилиндр. 
- телесный угол, он примерно определяет здесь, например, значение 
(при умножении на 
).
Если область – сплющенный эллипсоид, т.е.
, то 
, тогда 
.
С помощью потенциала можно найти напряжённость:
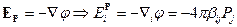
Это напряжённость поля однородно-поляризованного диэлектрика внутри объёма этого диэлектрика, т.е.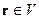 
.
Если диэлектрик находится во внешнем поле, то чтобы найти внутреннее поле такого диэлектрика надо к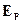 
ещё прибавить внешнее поле 
, где - однородное внешнее поле.
