Какие перемещения испытывают поперечные сечения балки при прямом изгибе?
Согласно гипотезе Бернулли поперечные сечения балки при прямом изгибе не искривляются, а лишь вертикально смещаются, поворачиваясь при этом относительно нейтральной линии на некоторый угол. Таким образом, перемещениями при изгибе являются вертикальное смещение (прогиб) сечений 
и угол поворота сечений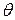 
, причем функция углов поворота 
связана с функцией прогибов 
дифференциальной зависимостью:
,
поэтому из двух функций перемещений основной является функция прогибов.
Как рассчитать балку на жесткость при изгибе?
Для этого необходимо определить максимальный прогиб балки 
, который можно найти, получив аналитическое выражение для функции прогибов . Но это достаточно сложная с математической точки зрения задача. Поэтому, чтобы оценить деформацию балки при изгибе рекомендуется следующее:
· определить прогибы в граничных незакрепленных сечениях балки;
· изобразить приближенный вид изогнутой оси балки, учитывая найденные значения перемещений, условия закрепления (закрепленные сечения не смещаются), а, также, согласуя направление выпуклости осевой линии с участками эпюры изгибающих моментов 
, на которых момент не меняет знак (эпюра располагается со стороны растянутых волокон относительно осевой линии);
· глядя на вид изогнутой оси балки, определить, в каком её сечении прогиб наибольший, найти методом Мора и проверить выполнение условия жесткости.
Что такое условие жесткости при изгибе?
Под условием жесткости понимается ограничение максимального вертикального смещения сечений балки величиной допускаемого перемещения:
,
где d max – величина максимального прогиба балки, [ d ] – допускаемое перемещение, обычно назначаемое из условий эксплуатации.
Как определить перемещение конкретного сечения балки при изгибе?
Перемещение конкретного сечения балки определяется методом Мора.
Алгоритм метода Мора. 
1. Для заданной балки построить эпюру изгибающих моментов от действия внешней нагрузки (грузовую эпюру).
2. Разгрузить балку от внешних нагрузок.
3. К сечению балки, перемещение которого необходимо определить, приложить в направлении перемещения единичную безразмерную сосредоточенную силу 
и построить от действия этой силы единичную эпюру изгибающих моментов 
;
4. Искомое перемещение определить путем «перемножения» грузовой эпюры на единичную эпюру , используя:
· либо интеграл Мора:
, (1)
где k – количество участков балки, 
– длина i-того участка, 
– функции грузового и единичного изгибающих моментов на i-том участке балки, соответственно, Е – модуль Юнга материала балки, 
– осевой момент инерции поперечного сечения. Таким образом, интегралы составляются и находятся для каждого участка балки, а результат суммируется;
· либо формулу Симпсона:
, (2)
где 
, 
, 
– ординаты грузовой эпюры изгибающего момента , взятые на левой границе, в средней точке и на правой границе i-того участка балки, соответственно; аналогично 
, 
, 
– ординаты единичной эпюры изгибающего момента , взятые на левой границе, в средней точке и на правой границе i-того участка балки. Остальные обозначения те же;
· либо формулу Верещагина:
, (3)
где 
– площадь грузовой эпюры изгибающего момента на i-том участке балки, 
– ордината единичной эпюры изгибающего момента , расположенная под центром тяжести грузовой эпюры i-го участка. Остальные обозначения те же.
Алгоритм расчета на жесткость балок при изгибе.
1. Построить эпюру изгибающего момента .
2. Определить перемещения граничных незакрепленных сечений балки методом Мора.
3. Изобразить приближенный вид изогнутой оси балки и определить максимальный прогиб .
4. Записать условие жесткости: и сделать вывод о его выполнении.
