Что такое главные центральные моменты инерции?
Это осевые моменты инерции Ix и Iy, вычисленные относительно главных центральных осей.
Что такое главные центральные оси?
Это оси, проходящие через центр тяжести сечения (центральные), относительно которых центробежный момент инерции равен нулю (главные). Ось симметрии всегда является главной центральной осью.
Зачем нужно уметь определять главные центральные моменты инерции?
Эти величины характеризуют жесткость поперечного сечения конструкции, работающей в условиях изгиба, и используются при расчетах такой конструкции на прочность и жесткость.
Чтобы научиться определять главные центральные моменты инерции надо знать 
!
1. Алгоритм определения центра тяжести сложного сечения: 
· Разделить сложную фигуру на i-простых фигур, координаты точек центра тяжести которых известны.
· Выбрать вспомогательную систему координат, в которой будет определяться центр тяжести всей фигуры. Рекомендации: для рациональности решения целесообразно оси вспомогательной системы координат провести через точку центра тяжести одной из составляющих простых фигур.
· Определить площади Аi и осевые статические моменты i-простых фигур относительно вспомогательных осей: Sxi=Ai×yCi; Syi=Ai×xCi, где хCi и yCi – координаты точек Ci центров тяжести простых фигур в системе вспомогательных осей.
· Вычислить координаты точки С центра тяжести всей фигуры по формулам:
ХС= 
; YC = 
2. Теорему о суммировании осевых моментов инерции:
Осевой момент инерции сложного сечения, состоящего из набора простейших, равен алгебраической сумме осевых моментов инерции простейших сечений, его составляющих, вычисленных относительно той же самой оси.
3. Формулы для определения главных центральных моментов инерции простейших сечений:
| Формы простейших сечений | Главные центральные моменты инерции | |||
|  , 
| |||
|  , 
| |||
| , 
| |||
| 
| |||
|  ,
| |||
|  , 
| |||
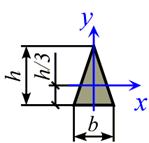
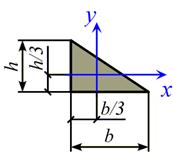
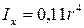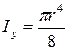
4. Теорему о преобразовании осевых моментов инерции при параллельном переносе осей:
Осевой момент инерции сечения относительно произвольной оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение квадрата расстояния между осями на площадь сечения:
, 
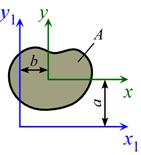
Алгоритм определения главных центральных моментов инерции сложного сечения
1. Определить положение центра тяжести сложного сечения согласно приведенному выше алгоритму;
2. Провести главные центральные оси сечения, одна из которых является осью симметрии, а другая, ей перпендикулярная, проходит через центр тяжести;
3. Провести главные центральные оси простейших сечений, составляющих сложное, и вычислить главные центральные моменты инерции этих сечений, воспользовавшись соответствующими формулами;
4. Найти расстояния между главной центральной осью всего сложного сечения и главной центральной осью каждого простейшего сечения, а затем определить моменты инерции каждого простейшего сечения относительно общей главной центральной оси, воспользовавшись теоремой о параллельном переносе осей;
5. Определить главные центральные моменты инерции сложного сечения по теореме о суммировании моментов инерции.
