Задача
Двухопорная балка постоянного поперечного сечения нагружена заданной системой поперечных сил и изгибающих моментов.

1. Для данной балки, изготовленной из пластичного материала с допускаемым напряжением 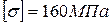 , подобрать из условия прочности двутавровое, прямоугольное (h/b=2) и круглое сечения. Дать заключение о рациональности формы сечения по расходу материала.
, подобрать из условия прочности двутавровое, прямоугольное (h/b=2) и круглое сечения. Дать заключение о рациональности формы сечения по расходу материала.
2. Для данной балки, изготовленной из хрупкого материала с допускаемыми напряжениями 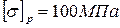 ,
, 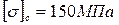 , определить из условия прочности характерный размер
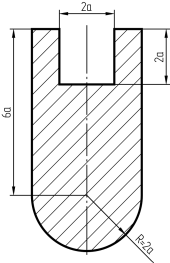
, определить из условия прочности характерный размер 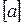 сложного поперечного сечения, предварительно решив вопрос о его рациональном положении. Принять:
сложного поперечного сечения, предварительно решив вопрос о его рациональном положении. Принять: 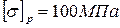 ,
, 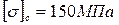 .
.
Решение
1. Рассмотрим первый случай, когда балка изготовлена из пластичного материала.
Построим эпюры поперечной силы  и изгибающего момента
и изгибающего момента  :
:
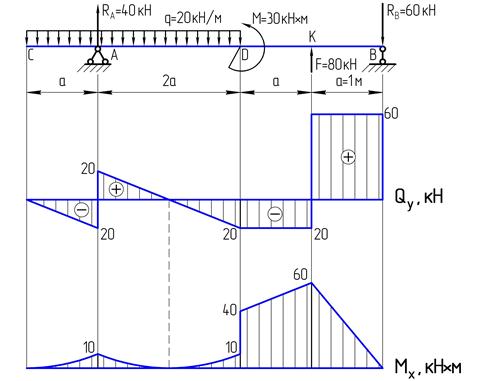
По эпюре  определяем положение опасного сечения – сечение К наиболее опасно,
определяем положение опасного сечения – сечение К наиболее опасно,  .
.
Подберем из условия прочности размеры трех форм сечений: двутаврового, прямоугольного и круглого. Для этого, прежде всего, найдем из условия прочности, каким минимальным моментом сопротивления должно обладать поперечное сечение балки:

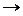
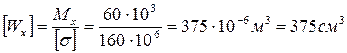 .
.
Далее, для каждой из трех форм сечений выразим момент сопротивления с геометрической точки зрения через характерный размер сечения и, приравняв его к расчетному моменту сопротивления 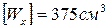 , определим характерный размер.
, определим характерный размер.
а) Двутавровое сечение:

Тонкостенные профили: двутавры, швеллеры, уголки выпускаются промышленностью определенных стандартных размеров. Номер профиля соответствует его высоте, выраженной в сантиметрах. Все характерные размеры таких профилей, а также их геометрические характеристики (в том числе и 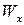 ) сведены в таблицы, которые называются «Сортаментом прокатных профилей» (см. Приложение 5, стр.119). Нам остается лишь по сортаменту указать номер двутавра, у которого момент сопротивления ближайший больший к расчетному: по сортаменту (ГОСТ 8239-89) подходит двутавр №27а, у которого
) сведены в таблицы, которые называются «Сортаментом прокатных профилей» (см. Приложение 5, стр.119). Нам остается лишь по сортаменту указать номер двутавра, у которого момент сопротивления ближайший больший к расчетному: по сортаменту (ГОСТ 8239-89) подходит двутавр №27а, у которого 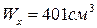 , а площадь сечения
, а площадь сечения 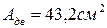 .
.
б) Прямоугольное сечение (h/b =2):
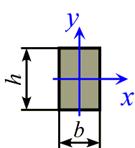
Нейтральная линия прямоугольника – главная центральная ось 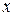 . Расстояние от нейтральной линии до наиболее удаленных точек сечения
. Расстояние от нейтральной линии до наиболее удаленных точек сечения 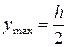 . Тогда
. Тогда 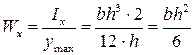 . Учитывая, что
. Учитывая, что 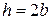 , выразим момент сопротивления прямоугольника через характерный размер b:
, выразим момент сопротивления прямоугольника через характерный размер b: 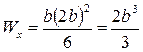 . Приравняв его к расчетному значению, находим минимально допустимый размер прямоугольника:
. Приравняв его к расчетному значению, находим минимально допустимый размер прямоугольника:
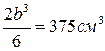
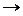
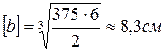 ,
,
тогда площадь прямоугольника: 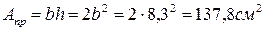 .
.
в) Круглое сечение:
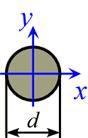
Здесь все аналогично: нейтральная линия – ось 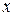 ,
, 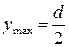 . Тогда
. Тогда
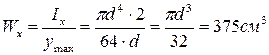
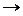
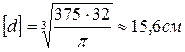 .
.
Площадь круглого сечения: 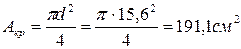 .
.
Наиболее рациональной формой сечения по расходу материала является та, которая имеет наименьшую площадь:
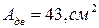 <
< 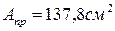 <
< 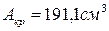 .
.
Следовательно, двутавровое сечение является наиболее рациональным.
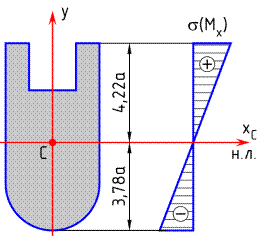
2. Рассмотрим балку из хрупкого материала и подберем из условия прочности характерный размер 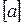 заданного сложного сечения, геометрические характеристики которого были определены в Теме 3.
заданного сложного сечения, геометрические характеристики которого были определены в Теме 3.
Нейтральная линия сечения – главная центральная ось 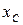 , проходящая через центр тяжести. Она делит всё сечение на две зоны – растянутых и сжатых волокон. Учитывая правило знаков для эпюры изгибающих моментов
, проходящая через центр тяжести. Она делит всё сечение на две зоны – растянутых и сжатых волокон. Учитывая правило знаков для эпюры изгибающих моментов  (строится на растянутых волокнах), легко определить расположение соответствующих зон в опасном сечении. На эпюре
(строится на растянутых волокнах), легко определить расположение соответствующих зон в опасном сечении. На эпюре  в опасном сечении К ордината
в опасном сечении К ордината 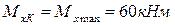 расположена выше осевой линии, следовательно, в этом сечении сверху от нейтральной линии расположены растянутые волокна, а снизу – сжатые. Определим расстояния от нейтральной линии до наиболее удаленных точек сечения в зонах растяжения и сжатия:
расположена выше осевой линии, следовательно, в этом сечении сверху от нейтральной линии расположены растянутые волокна, а снизу – сжатые. Определим расстояния от нейтральной линии до наиболее удаленных точек сечения в зонах растяжения и сжатия:  и
и 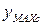 , учитывая положение центра тяжести сечения (см стр.31):
, учитывая положение центра тяжести сечения (см стр.31):
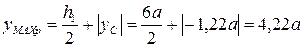
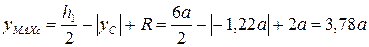
Решим вопрос о рациональности расположения сечения. Поскольку 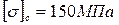 >
> 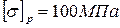 , а
, а 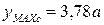 <
< 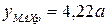 , значит сечение расположено нерационально и его нужно перевернуть на
, значит сечение расположено нерационально и его нужно перевернуть на  :
:
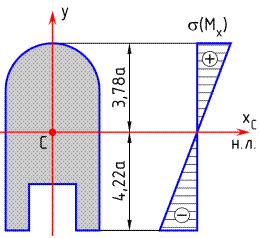
Теперь условие рациональности выполняется:
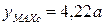 >
> 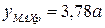 .
.
Определим положение опасного волокна в опасном сечении:
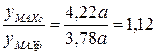 <
< 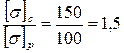 ,
,
следовательно, согласно условию (2) алгоритма опасным является наиболее растянутое волокно.
Запишем условие прочности для растянутого волокна и определим характерный размер сложного сечения 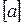 , учитывая ранее определенное значение момента инерции
, учитывая ранее определенное значение момента инерции 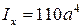 .
.
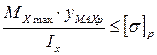
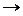
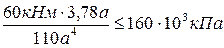
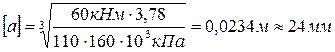 .
.
Задача решена. 






