Задача
Ступенчатый вал круглого поперечного сечения нагружен системой внешних крутящих моментов. Определить из условия прочности величину допускаемого диаметра сечения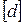 
, предварительно построив эпюры крутящего момента 
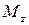и касательного напряжения 
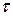. Проверить выполнение условия жесткости по абсолютным углам закручивания. Принять: 
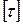=100 МПа, G= 
МПа,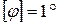 
.
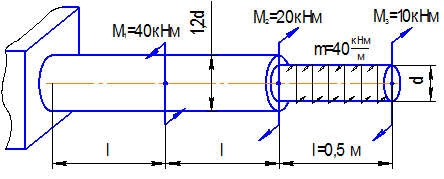
Решение
1. Построим эпюру крутящих моментов, используя метод сечений.
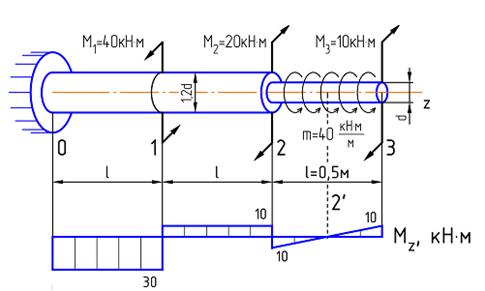
2. Определим касательные напряжения на каждом участке вала в долях диаметра d:
· на участке (0-1) (без распределенного момента) касательное напряжение есть величина постоянная, равная
;
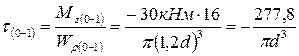· на участке (1-2) – аналогично:
;
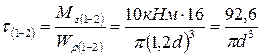· на участке (2-3) (с распределенным моментом) напряжение изменяется по линейному закону. Найдем 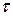на границах участка:
;
.
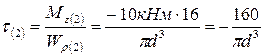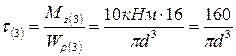3. По полученным значениям построим эпюру напряжений в долях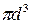 
, соблюдая характер зависимости на участках соответственно эпюре крутящих моментов.
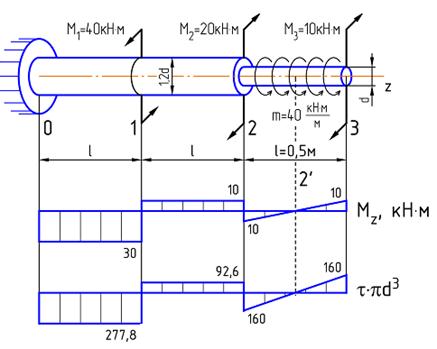
По эпюре напряжений видно, что опасным является участок (0-1):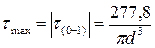 
.
4. Подставим полученное значение максимального напряжения в условие прочности и найдем минимально допустимый параметр d:
.
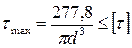
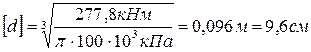5. Рассчитаем абсолютные углы закручивания участков стержня, приняв начало координат в жесткой заделке (сечение «0»). На участках с постоянным значением крутящего момента по длине функция углов закручивания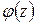 
изменяется по линейному закону и здесь для определения абсолютного угла закручивания можно использовать формулу: 
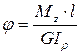, т.е. на участках (0-1) и (1-2)
;
,
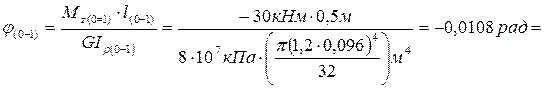
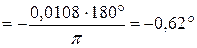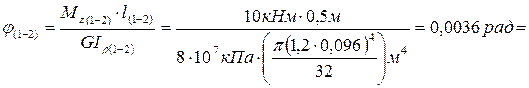
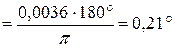на участке (2-3) крутящий момент изменяется по линейному закону, а функция 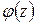по параболическому, и абсолютный угол закручивания определяется по интегральной формуле: 
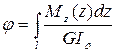, т.е.
.
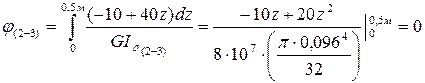Нулевое значение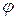 
здесь означает, что парабола на этом участке симметричная с одинаковыми значениями углов закручивания в граничных сечениях, а в среднем сечении участка (где 
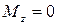) парабола имеет экстремум. Чтобы определить экстремальное значение угла закручивания, необходимо выделить на участке (2-3) подучасток, границами которого являются ближайшая к жесткой заделке граница участка (2-3), т.е. сечение (2), и экстремальное сечение, обозначим его 
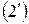. Таким образом, на выделенном подучастке 
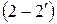, длиной 0,25м, абсолютный угол закручивания равен:
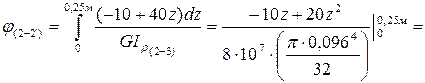
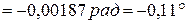
6. Определим углы закручивания характерных сечений (1), (2), (3) и экстремального сечения 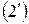относительно неподвижного сечения (0) и построим эпюру углов закручивания 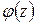на базе, параллельной продольной оси стержня:
,
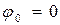
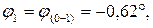
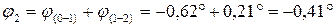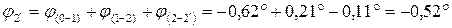
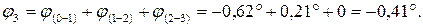
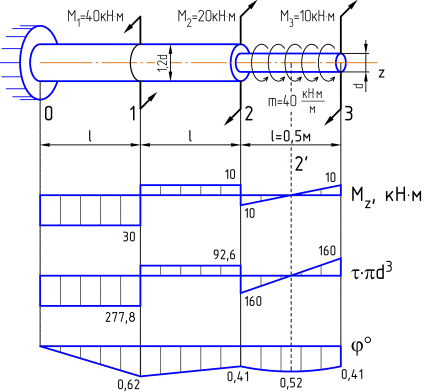
По эпюре видно, что максимальный по абсолютной величине угол закручивания возникает в сечении (1):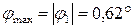 
.
7. Проверим выполнение условия жесткости: 
.
< 
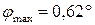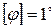, т.е. условие жесткости выполняется.
Задача решена. 
