Что такое условие прочности по допускаемому напряжению?
Известно, что в условиях прямого поперечного изгиба доминирующее значение в оценке прочности имеют нормальные напряжения, возникающие от внутреннего изгибающего момента, которые вычисляются по следующей формуле: 
, где Мх – величина внутреннего изгибающего момента в данном сечении, Wх – осевой момент сопротивления. Условием прочности по допускаемому напряжению при прямом изгибе считается выполнение следующего неравенства:
где 
– величина допускаемого напряжения, являющаяся справочной величиной или определяемая по характеристикам прочности для данной марки материала.
Как распределяется нормальное напряжение по поперечному сечению балки?
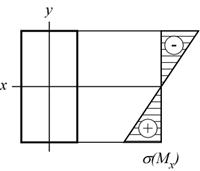
Нормальное напряжение 
по ширине сечения не изменяется, а по высоте сечения изменяется по линейному закону, причем оно равно нулю в точках нейтральной линии (горизонтальной главной центральной оси х) и принимает максимальное значение в точках, наиболее удаленных от нейтральной линии (опасных точках). Нейтральная линия делит все сечение на две зоны – зону растянутых (+) и сжатых (–) волокон.
Что такое осевой момент сопротивления?
Это геометрическая характеристика, которая зависит от формы и размеров поперечного сечения, а также от положения опасных точек в нем:
,
где 
– осевой момент инерции сечения, 
– расстояние от нейтральной линии до наиболее удаленных (опасных) точек сечения.
Чем с прочностной точки зрения отличаются пластичный и хрупкий материалы?
Пластичный материал одинаково сопротивляется напряжениям растяжения и сжатия, поэтому, для конструкций из пластичных материалов допускаемое напряжение принимается единое:
,
где 
– предел текучести материала,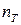 
– коэффициент запаса по текучести.
Хрупкий материал лучше сопротивляется нагрузкам сжатия и хуже нагрузкам растяжения, поэтому допускаемые напряжения здесь в зонах растяжения и сжатия разные:
, 
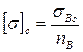, причем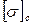 
> 
,
где 
, 
– пределы прочности материала при сжатии и при растяжении, соответственно, 
– коэффициент запаса по прочности.
Алгоритм расчета на прочность балок из пластичного материала 
1. Определить положение опасного сечения:
· Построить эпюры поперечной силы 
и изгибающего момента 
,
· По эпюре определить максимальное значение изгибающего момента.
2. Определить положение опасных точек в опасном сечении:
· Определить положение нейтральной линии,
· Найти – расстояние от нейтральной линии до наиболее удаленных (опасных) точек сечения.
3. Определить осевой момент сопротивления: .
4. Записать условие прочности: и решить его соответственно поставленной задаче.
Алгоритм расчета на прочность балок из хрупкого материала
1. Определить положение опасного сечения, построив эпюры поперечной силы и изгибающего момента .
2. Определить положение нейтральной линии в опасном сечении, определив положение его центра тяжести.
3. Решить вопрос о рациональности положения сечения, обеспечив соответствие: при 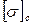> расстояние 
должно быть больше 
.
4. Определить момент инерции сечения относительно нейтральной линии.
5. Определить положение опасного волокна в опасном сечении, проведя следующий анализ:
· если 
> 
(1), то опасным является наиболее сжатое волокно,
· если < (2), то опасным является наиболее растянутое
волокно в опасном сечении.
6. Записать условие прочности и решить его соответственно поставленной задаче:
· 
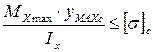в случае выполнения условия (1),
· 
в случае выполнения условия (2).
