Что такое условие прочности по допускаемому напряжению?
В условиях растяжения-сжатия в поперечных сечениях стержневой конструкции возникают нормальные напряжения под действием внутренней продольной силы, которые вычисляются по следующей формуле: 
, где N – величина внутренней продольной силы в данном сечении, A – площадь поперечного сечения. Условием прочности по допускаемому напряжению считается выполнение следующего условия:
,
где 
– величина допускаемого напряжения, являющаяся справочной величиной или определяемая по характеристикам прочности для данной марки материала, как: 
для пластичного материала или 
для хрупкого материала, где sT – предел текучести, sВ – предел прочности данной марки материала; nT – коэффициент запаса по текучести, nВ – коэффициент запаса по прочности.
Алгоритм расчета на прочность 
1. Определить положение опасного сечения:
· Построить эпюру продольной силы N
· Определить величину максимального нормального напряжения
2. Записать условие прочности: и решить его соответственно поставленной задаче.
Какие задачи можно решить из условия прочности?
1. Проверочная задача, когда известны геометрические размеры конструкции, условия нагружения, марка материала, из которой изготовлена конструкция, и необходимо проверить выполнение условия прочности.
2. Проектировочная задача, когда известны условия нагружения, соотношения геометрических размеров и форма поперечного сечения стержня, марка материала и необходимо определить допускаемую величину характерного размера поперечного сечения, удовлетворяющего условию прочности.
3. Задача об определении грузоподъемности конструкции, когда известны геометрические размеры, марка материала, закон нагружения конструкции и требуется определить величину допускаемой нагрузки, удовлетворяющей условию прочности.
4. Задача о подборе марки материала для изготовления конструкции, когда известны геометрические размеры и условия нагружения конструкции и требуется подобрать из условия прочности марку материала.
Что такое условие жесткости при растяжении-сжатии?
Под условием жесткости понимается ограничение максимального перемещения сечений стержневой конструкции в результате деформации растяжения-сжатия величиной допускаемого перемещения:
, или 
,
где d max – величина максимального перемещения поперечных сечений стержня вследствие деформации, [ d ] – допускаемое перемещение, обычно назначаемое из условий эксплуатации.
Величина d max может быть определена как накопленная алгебраическая сумма абсолютных деформаций участков стержня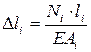 
, где 
– внутренняя продольная сила i-того участка, взятая с эпюры, 
– длина, 
– площадь поперечного сечения i-того участка соответственно, Е - модуль упругости 1-го рода (модуль Юнга).
Алгоритм расчета на жесткость.
1. Выбрать начало координат для отсчета перемещений поперечных сечений (если стержень имеет жесткую заделку, то рекомендуется принять начало координат в заделке).
2. Разделить стержень на участки, в пределах каждого из которых неизменны функция продольной силы и площадь поперечного сечения.
3. Начиная от начала координат, определить абсолютную деформацию каждого участка с учетом знака продольной силы.
4. Определить перемещение каждого характерного сечения стержня, как накопленную сумму абсолютных деформаций участков, предшествующих данному сечению: 
.
5. По значениям полученных перемещений рекомендуется построить эпюру, откладывая на базе, параллельной продольной оси стержня, величины перемещений в соответствующих сечениях стержня.
6. Записать условие жесткости в виде: и сделать вывод о его выполнении.
