Задача
Для данной балки построить эпюры поперечной силы и изгибающего момента.
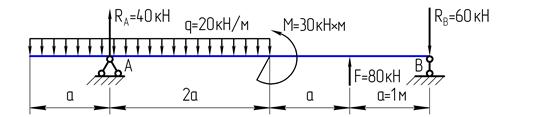
Решение:
Т.к. балка крепится на двух шарнирных опорах, то до начала построения эпюр необходимо определить реакции в опорах (практическое занятие по определению реакций опор на балках см. в Приложении 1, стр.55). Обозначим буквами опоры: шарнирно неподвижную «А», шарнирно подвижную «В». Для определения реакции в опоре А составим уравнение суммы моментов относительно точки опоры В: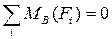 
.
Используем правило знаков моментов, принятое в Теоретической механике (раздел «Статика»): момент против часовой стрелки принимаем положительным и наоборот. В результате получим: 
. Подставив численное значение всех входящих величин, выразим из уравнения 
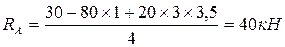. Для определения реакции в опоре В составим уравнение суммы моментов относительно точки опоры А: 
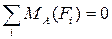, расписывая левую часть уравнения получим: 
, откуда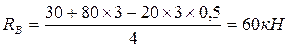 
. Для проверки правильности определенных реакции составим уравнение суммы проекций сил на вертикальную ось: 
или 
. Подставив численное значение сил, получим: 
, т.е. реакции найдены верно и можно приступать к построению эпюр.
Разделим балку на участки слева направо:
1-й участок от начала действия распределенной нагрузки до точки опоры А;
2-й участок от точки опоры А до конца действия распределенной нагрузки;
3-й участок от конца распределенной нагрузки до точки приложения силы F;
4-й участок от точки приложения силы F до конца балки.
Построение эпюры Qy
Проведем под расчетной схемой базу для эпюры Qy и разделим ее на участки, соответствующие участкам балки.
1-й участок
Левая граница участка: отсутствует сосредоточенная сила, поэтому на эпюре Qy будет ноль.
Состояние по длине участка: весь участок загружен распределенной нагрузкой, поэтому на эпюре будет наклонная прямая с угловым коэффициентом, равным q =20кН/м.
Правая граница участка: определим значение поперечной силы, умножив q на длину участка а, получим 20кН. Отложим это значение вниз от базы, т.е. со знаком «–» т.к. поворот вектора q относительно правой границы первого участка происходит против часовой стрелки. Соединим ординаты на левой и правой границе участка наклонной прямой.
2-й участок
Левая граница участка: здесь находится сосредоточенная сила RA, на величину которой надо сделать скачок в положительную сторону согласно правилу знаков. От ординаты равной –20 кН надо вверх отложить величину 40 кН. От базы эпюры сверху получится ордината, равная 20 кН.
Состояние по длине участка: весь второй участок также загружен распределенной нагрузкой, поэтому на эпюре должна быть наклонная прямая с угловым коэффициентом, равным q =20кН/м.
Правая граница участка: определим значение Qy, алгебраически складывая величину Qy на левой границе и величину равнодействующей распределенной нагрузки на 2-ом участке: 
. Соединим ординаты на левой 20кН и правой границе –20 кН наклонной прямой.
3-й участок
Левая граница участка: на левой границе находится сосредоточенный момент, на который поперечная сила не реагирует, т.е. значение –20 кН не изменится.
Состояние по длине участка: участок пустой, поэтому на эпюре будет параллельная прямая с ординатой –20кН.
Правая граница участка: ордината равная –20кН – конец прямой параллельной базе.
4-й участок
Левая граница участка: находится сосредоточенная сила F =80 кН, которая вызовет на эпюре скачок на эту величину вверх. Почему вверх 
? Потому, что сила F по ходу построения эпюры (слева направо) поворачивается по часовой стрелке. В результате в начале четвертого участка ордината поперечной силы будет равна 60 кН.
Состояние по длине участка: участок ничем не загружен, поэтому на эпюре должна быть прямая, параллельная базе.
Правая граница участка: здесь находится сосредоточенная сила RB, которая вызовет скачок на эпюре вниз на 60 кН.
Построение эпюры Мх
Эпюра Мх строится под эпюрой Qy. База эпюры предварительно делится на участки, соответствующие участкам балки.
1-й участок
Левая граница участка: отсутствует сосредоточенный внешний момент, поэтому на эпюре Мх будет ноль.
Состояние по длине участка: наличие равномерно распределенной нагрузки на эпюре Мх дает параболу, выпуклость которой направлена вниз (в сторону действия q). Парабола будет без экстремума, поскольку наклонная прямая на соответствующем участке Qy не пересекает базу. Строится по двум точкам – по значениям момента на левой и правой границе участка.
Правая граница участка: сделаем сечение по правой границе первого участка и оставим для определения момента в сечении «отрезанный» первый участок, загруженный только распределенной нагрузкой. Момент от нее и определит величину внутреннего момента. Заменим распределенную нагрузку ее равнодействующей, равной qa =20∙1=20 кН, мысленно поместим ее в точку центра тяжести площади, которую она занимает (это точка пересечения диагоналей прямоугольника), поэтому вектор равнодействующей будет проходить через середину длины участка. Тогда плечо у равнодействующей будет равно 0,5 метра, а момент в конце первого участка определится величиной равной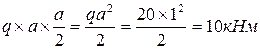 
, откладываем это значение в конце участка вверх, т.к. от действия распределенной нагрузки на отсеченную часть балки растянуты верхние волокна.
2-й участок
Левая граница участка: отсутствует сосредоточенный внешний момент, поэтому на эпюре Мх значение 10 кНм не изменится.
Состояние по длине участка: наличие равномерно распределенной нагрузки даст на эпюре Мх снова параболу выпуклостью вниз с экстремумом посередине участка, поскольку на соответствующем участке эпюры поперечной силы наклонная прямая пересекает базу в этом месте. Для определения экстремума сделаем сечение ровно посередине второго участка. Оставляя левую часть балки относительно сделанного сечения, на которой есть распределенная нагрузка и реакция RA, определим момент Мх:
Правая граница участка: т.к. парабола симметричная кривая, то очевидно, что в конце участка значение на эпюре момента должно быть такое же, как в начале (10 кНм на верхних волокнах). По трем точкам: 10 кНм, 0, 10 кНм строим параболу.
3-й участок
Левая граница участка: есть сосредоточенный внешний момент, равный 30 кНм, поэтому на эпюре Мх сделаем скачок вверх на величину момента. Почему вверх . Потому что, воздействуя моментом на балку слева, мы изгибаем ее так, что будут растянуты верхние волокна. Величина ординаты стала 40 кНм.
Состояние по длине участка: пустой, ничем не загружен. На эпюре Мх должна быть наклонная прямая с угловым коэффициентом, равным Qy этого участка, т.е. –20 кН. Построим прямую по двум точкам. Для этого определим значение момента на правой границе.
Правая граница участка: сделаем сечение по правой границе участка, оставим для определения момента правую часть балки относительно сделанного сечения, на которой есть только сила RB. Определим момент в сечении, как:
Почему +60 кНм . Потому, что, воздействуя на балку справа силой RB, мы изгибаем ее так, что будут растянуты верхние волокна. По полученным точкам на левой и правой границах участка соответственно 40 кНм и 60 кНм строим наклонную прямую.
4-й участок
Левая граница участка: отсутствует сосредоточенный внешний момент, поэтому на эпюре Мх значение 60 кНм не изменится.
Состояние по длине участка: пустой, ничем не загружен. На эпюре Мх должна быть наклонная прямая с угловым коэффициентом, равным Qy этого участка, т.е. 60 кН. Построим прямую по двум точкам. Для этого определим значение момента на правой границе.
Правая граница участка: находится в шарнирной опоре В, на которой отсутствует внешний момент. Такой шарнир называется свободным и в соответствующем сечении на эпюре Мх должен быть 0. По двум значениям момента на левой и правой границах участка (60 кНм и 0) строим наклонную прямую.
Проверка правильности построенных эпюр по дифференциальной зависимости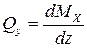 
Анализ эпюр проводим слева направо:
1-й участок: 
2-й участок: на первой половине 
, в точке пересечения 
и 
, на второй половине
3-й участок:
4-й участок:
Эпюры построены 
