Приведение квадратичной формы к каноническому виду с помощью выделения полных квадратов

Пусть L_n – n-мерное линейное пространство над полем Р и пусть на нём задана квадратичная форма j (а) = . Если n = 1, то форма уже имеет канонический вид, поэтому рассуждение можно вести индукцией по числу переменных. Пусть форму можно привести к каноническому виду, если число переменных не более (n – 1). Докажем его для n переменных. Возможны два случая.

1) Все коэффициенты a_кк = 0. Если все коэффициенты равны 0, то можно считать, что форма имеет канонический вид. Поэтому пусть хотя бы один из коэффициентов отличен от нуля. Не нарушая общности, можно считать, что a₁₂ ¹ 0. Сделаем преобразование координат: х₁ = у₁ – у₂, х₂ = у₁ + у₂, х₃ = у₃, …, х_n = у_n. В новых координатах

j (а) = a₁₂у₁² – a₁₂у₂² + y, где y не будет содержать у₁² и у₂², поэтому эти слагаемые ни с чем проведены быть не могут. Следовательно, достаточно рассмотреть случай

2) Хотя бы один коэффициент при квадратах переменных отличен от нуля. Пусть a₁₁¹ 0. Соберём в форме j (а) все слагаемые, содержащие х₁, вынесем a₁₁ за скобки, дополним полученную скобку до полного квадрата и компенсируем сделанные добавки.

a₁₁ ×() +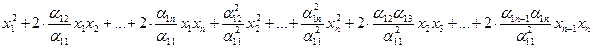

+ y (х₂, х₃, …,х_n), где y (х₂, х₃, …,х_n) – квадратичная форма от (n – 1) переменной. По предположению индукции форму y (х₂, х₃, …,х_n) можно с помощью преобразования координат (х₂, х₃, …,х_n) привести к каноническому виду. Дополнив это преобразование формулой у₁ = 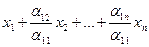, получим, что j (а) = .

Рассмотрим этот способ упрощения квадратичной формы на примере.

Пример. Привести к каноническому виду квадратичную форму

1) j = 3 х₁² + 5 х₂² + х₃² – 6 х₁х₂ + 9 х₁х₃ – 7 х₂х₃.

Решение. Коэффициент при х₁² отличен от нуля, поэтому соберём слагаемые, содержащие х₁ (они подчёркнуты), вынесем за скобки коэффициент при х₁² (т.е. 3) и дополним выражение в скобках до полного квадрата (за скобками компенсируем то, что добавили в скобках), получим

j = 3×(х₁² – 2 х₁х₂ + 3 х₁х₃ + х₂² + 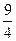х₃² – 3 х₂х₃) – 3 х₂² – 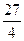х₃² + 9 х₂х₃ + 5 х₂² + х₃² – 7 х₂х₃ =

= 3(х₁ – х₂ + х₃)² + 2 х₂² – 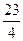х₃² + 2 х₂х₃. Так как коэффициент при х₂² отличен от нуля, то соберём слагаемые, содержащие х₂, вынесем коэффициент при х₂² за скобку и дополним выражение в скобках до полного квадрата. Получим

j = 3(х₁ – х₂ + х₃)² +2(х₂² + х₂х₃ + х₃²) – х₃² – 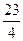х₃² =3(х₁ – х₂ + х₃)² + 2(х₂ + х₃)² – х₃². Сделаем преобразование координат:

у₁ = х₁ – х₂ + х₃, у₂ = х₂ + х₃, у₃ = х₃. В новых координатах получим, что

j = 3 у₁² + 2 у₂² – у₃².

Если квадратичная форма задана над полем действительных чисел, то сделав ещё одно преобразование координат: z₁ = 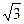у₁, z₂ = 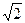у₂, z₃ = 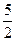у₃, получим нормальный вид данной формы j = z₁² + z₂² – z₃².

2) j = х₁х₃ + 2 х₂х₃ + 4 х₃х₄.

Решение. Так как данная квадратичная форма не содержит квадратов переменных, то сначала сделаем преобразование координат по формулам: х₁ = у₁ – у₃, х₂ = у₂, х₃ = у₁ + у₃, х₄= у₄. Получим j = (у₁ – у₃)(у₁ + у₃) + 2 у₂ (у₁ – у₃) + 4(у₁ + у₃) у₄ = у₁² – у₃² + 2у₁у₂ + 4у₁у₄ –2 у₂у₃ + 4 у₃у₄. Соберём слагаемые с у₁ (коэффициент при у₁² равен 1, поэтому ничего за скобки выносить не надо). Получим j = (у₁² + 2у₁у₂ + 4у₁у₄ + у₂² +4 у₄²+ 4 у₂у₄) – у₂² – 4 у₄² – 4 у₂у₄ – у₃² – 2 у₂у₃ + 4 у₃у₄ = = (у₁ + у₂ + 2 у₄)² – (у₂² + 2 у₂у₃ + 4 у₂у₄ + у₃² + 4 у₄² + 4 у₃у₄) + у₃² + 4 у₄² + 4 у₃у₄ – 4 у₄² – у₃² + 4 у₃у₄ = = (у₁ + у₂ + 2 у₄)² – (у₂ + у₃ + 2 у₄)² + 4 у₃у₄. Для преобразования последнего слагаемого снова нужно положить у₃ = z₃ – z₄, у₄ = z₃ + z₄. Отсюда z₃ = 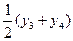, z₄ = 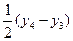.Итак, сделаем преобразование координат по формулам:

z₁ = у₁ + у₂ + 2 у₄, z₂ = у₂ + у₃ + 2 у₄, z₃ = 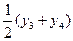, z₄ = 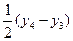. В новых координатах

j = z₁² – z₂² + 4 z₃² – 4 z₄².

Получили канонический вид данной квадратичной формы над полем действительных чисел.