IX. Билинейные и квадратичные формы

 

Линейные формы

Пусть L_n – n-мерное линейное пространство над полем Р и f –линейное отображение пространства L_n в поле Р (f: L_n ® Р).

Определение 58. Линейное отображение f: L_n ® Р называется линейной функцией или линейной формой, заданной на L_n.

Если е = (е₁, е₂,..., е_n) – базис в L_n, а – любой вектор из L_n, то а = х₁ е₁ + х₂ е₂ + … + х_n е_n, где х₁, х₂, …, х_n – любые элементы поля Р. Если f (е_к) = a_к, то f (а) = a₁х₁ + a₂х₂+ … + a_nх_n.

Следовательно, любую линейную форму можно задать в виде a₁х₁ + a₂х₂+ … + a_nх_n.

Легко показать, что множество всех линейных форм f: L_n ® Р является линейным пространством над полем Р.

 

Билинейные формы

Пусть L_n – n-мерное линейное пространство над полем Р.

Определение 59. Отображение f: (L_n ´ L_n) ® Р называется билинейной формой (или билинейной функцией), заданной на L_n, если для любых векторов а, в, с и любого элемента a Î Р выполняются условия:

f (а + в, с) = f (а, с) + f (в, с); f (а, в + с) = f (а, в) + f (а, с); f (a× а) = a× f (а).

(Иными словами, билинейная форма линейна по обоим переменным.)

Пусть в L_n зафиксирован базис е = (е₁, е₂,..., е_n), а = х₁ е₁ + х₂ е₂ + … + х_n е_n,

в = у₁ е₁ + у₂ е₂ + … + у_n е_n, f (е_к, е_р) = a_кр. Тогда из определения 58 следует

f (а, в) = f (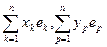) = = 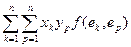, где a_кр – элементы поля Р.

Итак, f (а, в) = (55) – запись билинейной формы в координатах.

Матрица А =

называется матрицей данной билинейной формы. Если х и у – столбцы координат векторов а и в, то билинейную форму можно записать в матричном виде: f (а, в) = х Т× А × у (56)

Если е¹ = (е₁¹, е₂¹,..., е_n¹) – другой базис в L_n и Т – матрица перехода от базиса е к базису е¹, то столбцы координат векторов а и в в этих базисах связаны формулами х = Т×х¹, у =Т×у¹. Подставив в формулу (56), получим f (а, в) = (Тх¹) ^Т × А × (Ту¹) = (х¹)^Т×(Т ^Т× А × Т)× у¹. Следовательно, матрицы билинейной формы в разных базисах связаны формулой

А¹ = Т ^Т× А × Т (57)

Определение 60. Билинейная форма называется симметрической, если

f (а, в) = f (в, а) для любых векторов а и в. (57)

Очевидно, верно следующее утверждение:

Теорема 62. Билинейная форма является симметрической тогда и только тогда, когда она в любом базисе имеет симметрическую матрицу.

Теорема 63. В любом базисе евклидова пространства Е_n скалярное произведение векторов задаётся симметрической билинейной формой.

Доказательство. По формуле (42) скалярное произведение векторов а и в равно

(а, в) = х ^Т×Г × у. Матрица Г – симметрическая, поэтому, согласно формуле (56), скалярное произведение задано симметрической билинейной формой.

Квадратичные формы

Пусть L_n – n-мерное линейное пространство над полем Р и пусть на нём задана симметрическая билинейная форма f (а, в).

Определение 61. Симметрическая билинейная форма f (а, в) при условии а = в называется квадратичной формой, заданной на L_n (j (а) = f (а, в)). При этом f (а, в) и j (а) называются соответствующими друг другу.

Если в пространстве L_n задан базис е = (е₁, е₂, …, е_n) и а = х₁ е₁ + х₂ е₂ + … + х_n е_n, то, используя формулу (55), получим запись квадратичной формы в координатах

j (а) = (59)

Матрица квадратичной формы совпадает с матрицей соответствующей симметрической билинейной формы. Квадратичная форма в матричном виде запишется

j (а) = х ^Т× А × х (60)

Если в пространстве L_n зафиксирован базис, то между всеми квадратичными формами, заданными на L_n и всеми симметрическими квадратными матрицами порядка n устанавливается взаимнооднозначное соответствие. Сумма двух квадратичных форм является квадратичной формой. При умножении квадратичной формы на элемент поля Р получается тоже квадратичная форма. При сложении квадратичных форм складываются их матрицы. Если форма умножается на элемент поля Р, то на этот же элемент умножается и её матрица. Следовательно, множество всех квадратичных форм, заданных на L_n, есть линейное пространство, изоморфное линейному пространству квадратных симметрических матриц порядка n. Размерность этого пространства равна .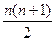

Так как квадратичная форма и соответствующая симметрическая билинейная форма имеют одну и ту же матрицу, то связь матриц А и А¹ в разных базисах задаётся формулой (56), т.е. А¹ = Т ^Т× А × Т, где Т – матрица перехода от первого базиса ко второму, Т ^Т – матрица, транспонированная для матрицы Т. Следовательно, в разных базисах квадратичная форма имеет более или менее сложные матрицы, а поэтому более или менее сложную запись в координатах. Поэтому возникает задача: найти в пространстве L_n такой базис, в котором квадратичная форма имела бы наиболее простой вид.

Определение 62. Если j (а) = a₁ х₁² + a₂ х ₂² + … + a_n х _n², то говорят, что квадратичная форма j (а) имеет канонический вид.

Если поле Р есть поле рациональных или действительных чисел и

j (а) = х₁² + х₂² + … + х_к² – х_к+1² – … – х_r²,

то говорят, что квадратичная форма имеет нормальный вид. В случае, когда Р = Снормальным видом квадратичной формы называют j (а) = х₁² + х₂² + …+ х_к² + х_к+1² +.+ х_r².

Теорема 64. Всякая квадратичная форма с помощью линейного невырожденного преобразования (преобразования координат) может быть приведена к каноническому виду.

Доказательство. Пусть j (а) – квадратичная форма, заданная на пространстве L_n. Пусть в L_n задан базис е и пусть в этом базисе j (а) = х ^Т× А × х. Матрица А –симметрическая, поэтому по теореме 60 существует такая ортогональная матрица Т, что матрица А¹ = Т^{– 1}× А × Т будет диагональной, причём на диагонали стоят собственные значения матрицы А (они все – действительные числа). Так как ортогональная матрица невырожденная, то существует такой базис е¹, что Т будет матрицей перехода от базиса е к базису е¹. Так как для ортогональной матрицы Т ^–1 = Т ^Т, то А¹ – матрица данной формы в базисе е¹. Итак, в базисе е¹ данная форма имеет канонический вид.

Замечание. Приведение симметрической матрицы к диагональному виду описано в примере пункта 8.3.

Теорема 65. Всякую квадратичную форму линейным невырожденным преобразованием можно привести к нормальному виду.

Доказательство. В теореме 64 доказано, что квадратичную форму можно привести к каноническому виду. Перенумеровав, если нужно переменные, будем считать, что первые r коэффициентов в каноническом виде отличны от нуля, а остальные (n – r) равны нулю.

1) В случае, когда Р = С сделаем преобразование координат по формулам (*).

(*)	Так как определитель этих формул отличен от нуля, то они задают преобразование координат. В новых координатах j (а) = у12 + у22 + … + уr2. Получили комплексный нормальный вид квадратичной формы. 2) Если Р = R, т.е. j (а) – действительная квадратичная форма, то в каноническом виде запишем сначала члены с положительными коэффициентами, затем – с отрицательными и, наконец, с нулевыми.
(**)	j (а) = a1 х12 + a2 х 22 + … + aк х к2 – aк+1 хк+12 – … – ar хr2 Сделаем преобразование координат по формулам (**), получим j (а) = у12 + у22 + … + ук2 – ук+12 – … – уr2. Но это и есть нормальный вид действительной квадратичной формы.

Пример. Привести к каноническому виду квадратичную форму

j = 2 х₁х₂ + 2 х₁х₃ – 2 х₁х₄ – 2 х₂х₃ + 2 х₂х₄ + 2 х₃х₄.

Решение. Матрица данной квадратичной формы

А =	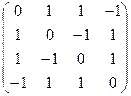Для решения задачи эту матрицу нужно привести к диагональному виду. Это было сделано в примере пункта 8.3. Собственные значения этой матрицы l1 = l2 = l3 = 1, l4 = – 3. Базис из собственных векторов был найден е11 = е21 = ,
А1 =	е31 = , е41 = (1, –1, –1, 1). В этом базисе квадратичная форма будет иметь матрицу А1. Матрицей перехода от исходного базиса к базису е1 будет матрица Т.
Т =	Следовательно, форма j будет иметь следующий канонический вид j = х12 + х22 + х32 – 3 х42.