Теорема 39. Линейное преобразование j линейного пространства Ln над полем Р имеет в базисе е = (е1, е2,..., еn) диагональную матрицу тогда и только тогда, когда все векторы базиса являются собственными векторами преобразования j.
Доказательство. Þ Пусть матрица А линейного преобразования j в базисе е – диагональная. Тогда j (ек) = lк для любого к = 1, 2, …, n. Но это значит, что все базисные векторы – собственные..
Ü Пусть все базисные векторы – собственные. Тогда j (ек) = lк. Следовательно, в к -ом столбце матрицы этого преобразования на всех местах, кроме к -го, стоят нули и акк = lк. Отсюда и следует, что матрица преобразования – диагональная.
Следствие. Квадратная матрица n -го порядка подобна диагональной тогда и только тогда, когда для соответствующего этой матрице линейного преобразования существует базис из собственных векторов.
Определение 42. Говорят, что линейное преобразование j линейного пространства Ln над полем Р имеет простой спектр, если все его характеристические корни различны и принадлежат полю Р.
Теорема 40. Если линейное преобразование j линейного пространства Ln над полем Р имеет простой спектр, то в Ln существует такой базис, в котором это преобразование имеет диагональную матрицу.
Теорема 41. Пусть А – квадратная матрица с элементами из поля Р. Если все характеристические корни матрицы А различны и принадлежат полю Р, то эта матрица подобна диагональной.
VII. ЕВКЛИДОВЫ ПРОСТРАНСТВА
Скалярное произведение векторов, его свойства. Определение и примеры евклидовых и унитарных пространств
Пусть L – линейное пространство над полем Р. В L определены две алгебраические операции: сложение векторов и умножение векторов на элементы поля Р, Введём ещё одну внутреннюю алгебраическую операцию, являющуюся обобщением скалярного произведения геометрических векторов. В основу определения этой операции положим те свойства скалярного произведения геометрических векторов, которые были получены в аналитической геометрии. При этом определения скалярного произведения в случае, когда поле Р является полем действительных чисел, отличается от случая, когда Р = С.
Определение 43
| а) Р = R Будем говорить, что в действительном линейном пространстве L определено скалярное произведение векторов, если каждой упорядоченной паре векторов а и в из L поставлено в соответствие число (а, в) Î R, удовлетворяющее следующим требованиям (аксиомам скалярного произведения): 1. (а, в) = (в, а) для любых а и в из L; 2. (а + в, с) = (а, с) + (в, с) для любых а, в, с из L; 3. (aа, в) = a (а, в) для любых а и в из L и любого a Î R; 4. (а, а) > 0, если а ¹ 0; (а, а) = 0, если а = 0. | б) Р = С
Будем говорить, что в комплексном линейном пространстве L определено скалярное произведение векторов, если каждой упорядоченной паре векторов а и в из L поставлено в соответствие число (а, в) Î С, удовлетворяющее следующим требованиям (аксиомам скалярного произведения):
1.  =  для любых а и  из L;
2. (а + в, с) = (а, с) + (в, с) для любых а, в, с из L;
3. (aа, в) = a (а, в) для любых а и в из L и любого a Î С;
4. (а, а) Î R и (а, а) > 0, если а ¹ 0; (а, а) = 0, если а = 0.
|
Скалярное произведение векторов можно обозначать (а, в) или а×в.
Свойства скалярного произведения.
| а) Р = R 10. (а, aв) = a (а, в) для любых а и в из L и любого a Î R; 20. (a × а,b× в) = a×b (а, в) для любых а и в из L и любых a, b Î Р; 30. (a × а + b× в, gс) = ag× (а, с) + bg (в, с) для любых а, в и с из L и любых a, b, g Î Р; 40. (а, 0) = 0 для любого вектора а Î L. | б) Р = С
10. (aа, в) =  × (а, в) для любых а и в из L и любого a Î С;
20. (a × а,b× в) = a×  (а, в) для любых а и в из L и любых a, b Î С;
30. (a × а + b× в, gс) = a×  (а, с) + b (в, с) для любых а, в и с из L и любых a, b, g Î С;
40. (а, 0) = 0 для любого вектора а Î L.
|
Определение 44. Действительное линейное пространство, в котором определено скалярное произведение векторов, называется евклидовым пространством.
Определение 45. Комплексное линейное пространство, в котором определено скалярное произведение векторов, называется унитарным пространством.
Так как и евклидово и унитарное пространства являются линейными пространствами, то для них верно всё то, что было сказано об этих пространствах. Но введение скалярного произведения позволяет ввести в этих пространствах метрику. В частности n -мерное линейное пространство, в котором введено скалярное произведение векторов, называется n-мерным евклидовым (или унитарным) пространством. Евклидово n -мерное пространство будем обозначать Еn (унитарное пространство - Un).
Примеры евклидовых пространств.
1. Пусть L – множество всех непрерывных на промежутке [a, b] действительных функций. Это множество является линейным пространством. Скалярное произведение определим по следующему правилу. Если f и g – две непрерывные на [a, b] функции, то пусть (f,g) =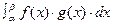 
. Из свойств определённого интеграла следует, что все требования определения 43 (а) выполняются. Следовательно, если в пространстве всех непрерывных на промежутке [a, b] действительных функций ввести указанным способом скалярное произведение, то оно становится евклидовым пространством.
2. Пусть М2 – множество квадратных матриц с действительными элементами, это множество является линейным пространством на полем R. Определим скалярное произведение формулой 
. Легко проверить, что все требования определения 43 (а) выполняются. Множество М2 стало евклидовым пространством.
3. Пусть М2 – множество квадратных матриц с комплексными элементами, это множество является линейным пространством на полем С. Определим скалярное произведение формулой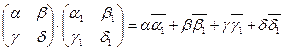 
. Легко проверит, что все требования определения 43 (б) выполняются. Получили пример унитарного пространства.
Определение 46. Множество М элементов евклидова пространства Е называется подпространством пространства Е, если оно само является евклидовым пространством относительно того же скалярного произведения, что и Е. Аналогично определяется подпространство унитарного пространства.
