Пространство решений системы линейных однородных уравнений

Пусть дана система (30) линейных однородных уравнений с коэффициентами из поля Р.

(30)	Так как столбец свободных членов в матрице А1 этой системы состоит только из нулей, то rang A = rang A1, т.е. система линейных однородных уравнений всегда совместна. В частности она всегда имеет нулевое решение. Рассмотрим множество всех возможных решений системы (30).

Пусть a =(a₁, a₂, …, a_n) и b =(b₁, b₂, …, b_n) – любые два из них. Их можно рассматривать, как векторы в арифметическом n-мерном пространстве над полем Р. Пусть l – любой элемент поля Р. Тогда a + b = (a₁ + b₁, a₂ + b₂, …, a_n + b_n), l ×a = (la₁, la₂, …, la_n). Подставим компоненты этих векторов в произвольное s -е уравнение системы (30). Получим 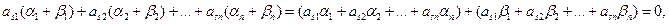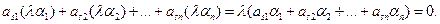Итак, если a и b – любые два решения системы (30) и l – любой элемент поля Р, то a + b и l ×a тоже являются решением этой системы. Но тогда из теоремы 14 следует

Теорема 27. Множество решений системы линейных однородных уравнений с n переменными есть линейное подпространство арифметического пространства А_n.

Теорема 28. Размерность пространства решений системы линейных однородных уравнений равна n – r, где n – число неизвестных, r – ранг матрицы системы.

Доказательство. Пусть L – пространство решений системы (30). Тогда L Ì А_n. Пусть a = (a₁, a₂, … a_r, a_r+1, …, a_n) – произвольное решение системы. Пусть (a_r+1, …, a_n) – набор свободных неизвестных, соответствующий этому решению. Множество всех возможных наборов свободных неизвестных есть арифметическое (n – r)-мерное пространство А_n–r. Зададим отображение j: L ® А_n–r по правилу

a = (a₁, a₂, … a_r, a_r+1, …, a_n) ® j (a)= (a_r+1, …, a_n).

Покажем, что j – изоморфизм (определение 24). Для этого нужно проверить три условия.

1. Покажем, что j – взаимнооднозначное отображение. Решению a = (a₁, a₂, … a_r, a_r+1, …, a_n) соответствует только один набор (a_r+1, …, a_n), следовательно, j – однозначное отображение. Обратно, если задать элемент (a_r+1, …, a_n) из А_n–r, то по теореме Крамера найдётся только один набор (a₁, a₂, … a_r) искомых неизвестных, т.е. каждый элемент j (a) из А_n–r соответствует единственному элементу из L.

2. j(l a) = (la_r+1, …, la_n) = l× (a_r+1, …, a_n) = l×j (а).

3. j (а + в) = (a_r+1 + b_r+1, …,a_n + b_n) = (a_r+1, …, a_n) + (b_r+1, …, b_n) = j (а) + j (в).

Итак, пространство решений системы линейных однородных уравнений изоморфно арифметическому (n – r)-мерному пространству. Следовательно, размерность L равна (n – r).

Определение 29. Базис пространства решений системы линейных однородных уравнений называется её фундаментальной системой решений.

Так как при изоморфизме базис пространства А_n–r соответствует базису пространства L, то для того. чтобы найти фундаментальную систему решений для системы (30), достаточно выбрать (n – r) линейно независимых наборов свободных неизвестных и для каждого из них найти решение данной системы.

Следствие. Если а₁, а₂, …, а_n–r фундаментальная система решений системы линейных однородных уравнений (30) и С₁, С₂, …, С_n–r – произвольные элементы поля Р, то С₁ а₁ + С₂ а₂ + … + С_n–r а_n–r – общее решение этой системы.