Связь решений однородной и неоднородной систем линейных уравнений

 

Пусть (25) произвольная система линейных неоднородных уравнений с коэффициентами из поля Р. Если в этой системе все свободные члены заменить нулями, то полученная система линейных однородных уравнений называется соответствующей однородной системой (это система (30)). Решения систем (25) и (30) удовлетворяют следующим свойствам:

(30)	10. Сумма решений данной неоднородной и соответствующей однородной системы линейных уравнений есть решение данной неоднородной системы. Пусть а – частное решение системы (25) и с – частное решение системы (30). Рассмотрим вектор (а + с).

Системы (25) и (30) в векторной форме имеют вид А× х = в (31) и А× х = 0 (32). По условию А× а = в, А× с = 0. Следовательно, А× (а + с) = А× а + А× с = в + 0 = в. Следовательно, (а + с) – решение уравнения (31), а поэтому и системы (25).

2⁰. Разность двух решений неоднородной системы линейных уравнений есть решение соответствующей однородной системы.

Пусть а и с – решения системы (25), а следовательно, и уравнения (31), т.е. А× а = в и А× с = в. Тогда А× (а – с) = А× а – А× с = в – в = 0, т.е. (а – с) – решение уравнения (32), а поэтому и системы (30).

3⁰. Если а – фиксированное частное решение системы (25), а с пробегает все решения системы (30), то (а + с) пробегает все решения системы (25).

Согласно 1⁰, при любом с вектор (а + с) будет решением системы (25). Если d – любое решение системы (25), то, согласно 2⁰, разность (d – а) будет решением системы (30). Обозначив (d – а) = с, получим d = (а + с).

Теорема 29. Если а – частное решение линейной неоднородной системы уравнений и а₁, а₂, …, а_n–r – фундаментальная система решений соответствующей однородной системы уравнений, то общее решение данной неоднородной системы имеет вид

d = а + С₁ а₁ + С₂ а₂ + … + С_n–r а_n–r, где С₁, С₂, …, С_n–r – любые элементы поля Р.

(Иными словами, общее решение системы линейных неоднородных уравнений равно сумме частного решения этой системы и общего решения соответствующей однородной системы.)

Доказательство является следствием предыдущих свойств.

 

Задание подпространств конечномерного линейного пространства с помощью систем линейных уравнений

Пусть дано n- мерноелинейное пространство L и пусть в нём зафиксирован базис е = (е ₁, е₂, …, е_n). Пусть М – линейное подпространство в L.

Определение 30. Будем говорить, что система линейных уравнений задаёт подпространство М, если этой системе удовлетворяют координаты всех векторов из М и не удовлетворяют координаты никаких других векторов.

Из свойств решений однородной системы линейных уравнений следует, что любая однородная линейная система уравнений ранга r с n переменными задаёт в любом n- мерном пространстве L_n (если в нём зафиксирован базис) (n–r)-мерное линейное подпространство.

Справедливо и обратное утверждение. А именно, имеет место следующая теорема.

Теорема 30. Если в линейном n- мерном пространстве L_n зафиксирован базис, то любое его к -мерное линейное подпространство можно задать системой линейных однородных уравнений с n неизвестными ранга (n – к).

Доказательство. Пусть в L_n зафиксирован базис е = (е ₁, е₂, …, е_n). Пусть L_к – линейное к -мерное подпространство в L_n. Выберем в L_к любой базис а = (а₁, а₂, …, а_к). Пусть В матричной форме а = е × А, где А = .

Так как а – базис, то ранг матрицы А равен к.

Если d – любой вектор, то d Î L_к Û d = с₁ а₁ + с₂ а₂ + … + с_к а_к, где с₁, с₂, …, с_к независимо друг от друга пробегают все элементы поля Р. Их называют параметрами. В матричном виде d = а × с, где с – столбец параметров. Отсюда d = е× (А ×с). Если х – столбец координат вектора а в базисе е, то d = е×х. Отсюда, е×х = е× (А ×с) и х = А ×с. Распишем в координатном виде.

Получили параметрические уравнения, определяющие Lк. После исключения параметров получится система (n – к) линейных однородных уравнений. Векторы а1, а2, …, ак являются её линейно независимыми решениями. Все остальные решения являются их линейными комбинациями.

Следовательно, система векторов (а₁, а₂, …, а_к) будет фундаментальной системой решений полученной системы уравнений и поэтому ранг этой системы уравнений равен (n – к).

Пример. В пространстве L₅ зафиксирован базис е = (е ₁, е₂, е₃, е₄, е₅). Найти систему линейных однородных уравнений, задающих L₃ = < а₁, а₂, а₃ >, если а₁ = (1, –2, 2, 0, 1), а₂ = (0, 4, 7, 0, 1), а₃ = (–2, 3, –1, 0, 0).

Решение. Найдём ранг системы векторов (а₁, а₂, а₃). Для этого достаточно найти ранг матрицы . Минор . Окаймляющий минор 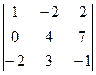¹ 0, следовательно, ранг матрицы равен 3, т.е. векторы а₁, а₂, а₃ линейно независимы и подпространство L₃ – трёхмерное. Согласно доказанной теоремы, оно может быть задано системой линейных однородных уравнений ранга 2.

d Î L₃ Û d = с₁ а₁ + с₂ а₂ + с₃ а₃. Отсюда d Î L₃ Û х₁ = с₁ – 2с₃, х₂ = –2с₁ + 4с₂ + 3с₃, х₃ = 2с₁ + 7с₂ – с₃ , х₄ = 0, х₅ = с₁ + с₂. Если из первого второго и пятого уравнений выразить с₁, с₂ и с₃ и подставить их в третье и четвёртое уравнения, то получим следующую систему

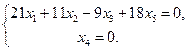
Замечание. Очевидно, система, задающая данное подпространство, определяется не единственным образом. К найденным уравнениям можно добавлять новые уравнения, являющиеся их линейными комбинациями.

 

VI. ЛИНЕЙНЫЕ ОПЕРАТОРЫ