Определение 24. Два линейных пространства L и L1 над одним и тем же полем Р называются изоморфными, если существует такое взаимнооднозначное отображение j: L ® L1, что для любых векторов а и в из L и любого элемента l Î Р выполняются условия: j(а + в) = j(а) + j(в), j(l а) = lj(а).
Отображение j называется изоморфизмом.
Определение 24 можно заменить следующим эквивалентным определением.
Определение 25. Два линейных пространства L и L1 над одним и тем же полем Р называются изоморфными, если существует такое взаимнооднозначное отображение j: L ® L1, что для любых векторов а и в из L и любых элементов l, m Î Р выполняется условие: j(l а + m в) = lj(а) + mj(в).
Свойства изоморфизма.
1. j(0) = 01, где 0 и 01 – нулевые вектора в пространствах L и L1 соответственно.
2. Если а1, а2, …, ак – любая система векторов из L и j(а1) = а11, j(а2) = а21, …, j(ак) = ак1, то j(a1 а1 + a2 а2 + … + aк ак) = a1 а11 + a2 а21 + … + aк ак1.
3. Если а1, а2, …, ак –линейно независимая система векторов из L и j(а1) = а11, j(а2) = а21, …, j(ак) = ак1, то система векторов а11, а21, …, ак1 – линейно независима в L1.
4. Если а1, а2, …, ак –линейно зависимая система векторов из L и j(а1) = а11, j(а2) = а21, …, j(ак) = ак1, то система векторов а11, а21, …, ак1 – линейно зависима в L1.
5. Если L – n- мерное линейное пространство, то L1 – тоже n -мерное линейное пространство.
6. При изоморфизме образом любого базиса из L является базис из L1.
Примеры изоморфных пространств.
1. Арифметическое линейное пространство Аn над полем Р изоморфно пространству многочленов степени не выше (n – 1) с коэффициентами из поля Р.
2. Пространство квадратных матриц порядка n с элементами из поля Р изоморфно арифметическому линейному пространству размерности n2 над полем Р.
V. РАНГ МАТРИЦЫ. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Ранг матрицы
Пусть Р некоторое фиксированное поле и пусть А =  произвольная матрица размерности m ´ n. Каждый столбец матрицы можно рассматривать как m- мерныйвектор из m -мерного арифметического пространства Аm. Тогда система столбцов матрицы будет системой m- мерныхвекторов а1 = (а11, а21, …, аm1), а2 = (а12, а22, …, аm2), …, аn = (а1n, а2n, …, аmn).
произвольная матрица размерности m ´ n. Каждый столбец матрицы можно рассматривать как m- мерныйвектор из m -мерного арифметического пространства Аm. Тогда система столбцов матрицы будет системой m- мерныхвекторов а1 = (а11, а21, …, аm1), а2 = (а12, а22, …, аm2), …, аn = (а1n, а2n, …, аmn).
Определение 26. Столбцевым рангом матрицы А называется ранг системы её векторов – столбцов.
По аналогии со столбцами каждую строку матрицы А можно рассматривать как n -мерный вектор из n- мерного арифметического пространства Аn.
Определение 27. Строчным рангом матрицы А называется ранг системы её векторов – строк.
Теорема 18. Столбцовый ранг матрицы равен наибольшему порядку среди отличных от нуля её миноров.
Доказательство. Если все элементы матрицы – нули поля Р, то все её столбцы – нулевые вектора. Ранг этой системы векторов равен нулю. В матрице А все миноры первого порядка, все миноры второго порядка и т.д. равны нулю. Можно считать, что максимальный порядок отличных от нуля миноров равен нулю.
Пусть в матрице А не все элементы равны нулю, тогда в матрице есть отличные от нуля миноры. Выберем минор наибольшего порядка среди всех отличных от нуля. При перестановке столбцов ранг системы векторов-столбцов не изменится. При перестановке строк матрицы изменится только порядок координат векторов (при этом у всех векторов одинаково). Следовательно, эта перестановка тоже не изменит ранга системы векторов-столбцов. Переставим, если нужно, строки и столбцы матрицы так, чтобы выбранный нами минор М располагался в левом верхнем углу матрицы. Пусть его порядок равен к. Рассмотрим систему векторов-столбцов матрицы А. Обозначим их а1, …, ак, ак+1, …, аn. Векторы а1, …, ак линейно независимы, иначе выбранный нами минор был бы равен нулю. Покажем, что любой другой вектор-столбец через них линейно выражается. Для этого окаймим выбранный минор любым столбцом с номером к +1, к + 2, …, n и любой
а1, …, ак, ак+1, …, аn
А = 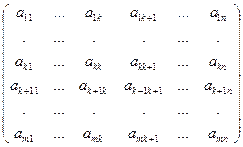
| строкой. Если номер этой строки не больше к, то полученный определитель будет иметь две одинаковых строки, поэтому равен нулю. Если номер окаймляющей строки больше к, то этобудет минор матрицы А порядка (к + 1), поэтому равен нулю по условию. Итак, определитель 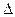 равнее нулю при любом s, равном к + 1, …, n и любом р, равном 1, 2, …, m. равнее нулю при любом s, равном к + 1, …, n и любом р, равном 1, 2, …, m.
|
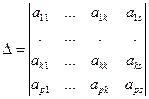 = 0. = 0.
| Разложим 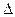 по последней строке, получим по последней строке, получим
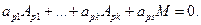 Так как М ¹ 0, то
Так как М ¹ 0, то 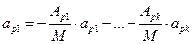 . .
|
Если номер столбца s зафиксирован, то алгебраические дополнения Ар1, …, Арк не меняются при изменении номера строки р. Следовательно, аs = 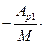 а1 – … –
а1 – … – 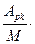 ак. Итак, любой вектор-столбец матрицы А линейно выражается через первые к её столбцов. Следовательно, столбцовый ранг матрицы равен к, т.е. наибольшему порядку отличных от нуля её миноров.
ак. Итак, любой вектор-столбец матрицы А линейно выражается через первые к её столбцов. Следовательно, столбцовый ранг матрицы равен к, т.е. наибольшему порядку отличных от нуля её миноров.
Следствие. Строчный ранг матрицы равен её столбцовому рангу.
Доказательство. Транспонируем матрицу А. При этом векторы-строки матрицы А станут векторами-столбцами транспонированной матрицы АТ. П ри транспонировании матрицы транспонируются и все её миноры. Так как при транспонировании определитель не меняется, то максимальный порядок отличных от нуля миноров в матрицах А и АТ один и тот же. По доказанной теореме столбцовые ранги этих матриц равны. Отсюда и следует утверждение следствия.
Так как столбцовый и строчный ранги матриц равны, то можно дать определение:
Определение 28. Рангом матрицы называется ранг системы её векторов-столбцов (или векторов-строк).
Из теоремы о ранге матрицы следует, что если мы найдём в матрице А минор М к- го порядка, отличный от нуля, то среди миноров (к + 1)-го порядка достаточно рассмотреть только те, которые получаются окаймлением минора М. Если они все равны нулю, то ранг матрицы равен к. В дальнейшем минор наибольшего порядка среди отличных от нуля будем называть базисным минором.
Пример. Найти ранг матрицы А = 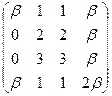 в зависимости от b.
в зависимости от b.
Решение. Так как не все элементы матрицы равны нулю, то её ранг не меньше 1. Так как второй т третий столбцы одинаковы, то один из ни можно отбросить и находить ранг матрицы А1 = 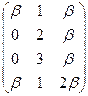 . Из миноров второго порядка только один
. Из миноров второго порядка только один 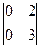 не содержит b, но этот минор равен 0. Рассмотрим минор М1 =
не содержит b, но этот минор равен 0. Рассмотрим минор М1 = 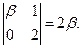 При b = 0 матрица А1 имеет вид
При b = 0 матрица А1 имеет вид  . В ней только один ненулевой столбец, следовательно, её ранг равен 1. Если
. В ней только один ненулевой столбец, следовательно, её ранг равен 1. Если 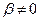 , то М1 ¹ 0, т.е. ранг матрицы не меньше 2. Минор М1 можно окаймить третьей строкой и третьим столбцом или четвёртой строкой и третьим столбцом. Получим М2 =
, то М1 ¹ 0, т.е. ранг матрицы не меньше 2. Минор М1 можно окаймить третьей строкой и третьим столбцом или четвёртой строкой и третьим столбцом. Получим М2 = 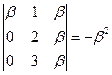 . Так как
. Так как 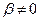 , то М2 ¹ 0. В матрице А1 миноров 4-го порядка нет, поэтому rang A = rang A1 = 3.
, то М2 ¹ 0. В матрице А1 миноров 4-го порядка нет, поэтому rang A = rang A1 = 3.
Итак, при b = 0 rang A, при b ¹ 0 rang A = 3.
Теорема 19. Элементарные преобразования матрицы не меняют её ранга.
Доказательство следует из того, что при элементарных преобразованиях матрицы мы получаем эквивалентные системы её векторов-строк.






