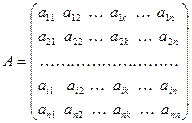
Определение. Минором элемента  квадратной матрицы A называется определитель матрицы, полученной из матрицы A вычеркиванием i-ой строки и k-ого столбца. Обозначение:
квадратной матрицы A называется определитель матрицы, полученной из матрицы A вычеркиванием i-ой строки и k-ого столбца. Обозначение:  .
.
Выражение вида: 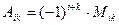 , будем называть алгебраическим дополнением элемента
, будем называть алгебраическим дополнением элемента  матрицы A.
матрицы A.
Теорема. Определитель матрицы A n-ого порядка равен сумме произведений элементов произвольной строки (столбца) на соответствующие алгебраические дополнения:
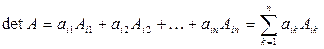 - разложение по строке;
- разложение по строке;
 - разложение по столбцу.
- разложение по столбцу.
Доказательство.
Воспользуемся свойствами 5, 2 и определением определителей:
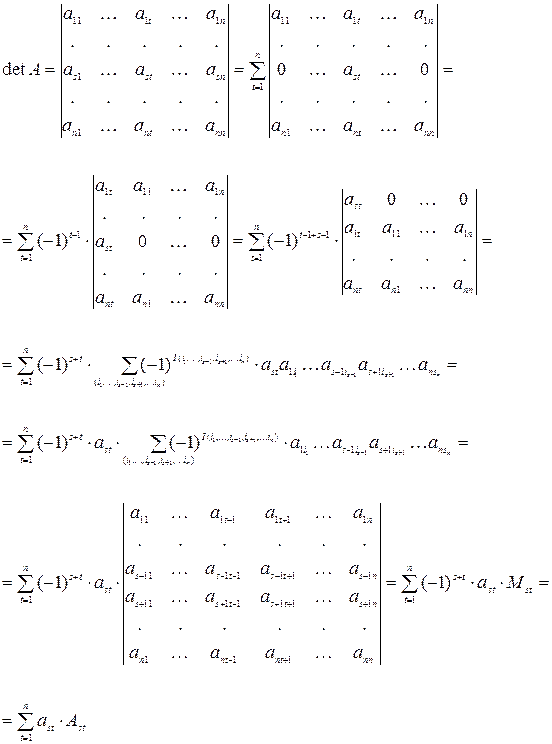
Формула разложения по столбцу доказывается аналогично.
Пример.
Вычислим определитель разложением по 1-й строке: 
Теорема. Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения элементов другой строки (столбца) равна 0, т.е. справедлива формула:

(здесь  - символ Кронекера).
- символ Кронекера).
Доказательство.
При i=j утверждение совпадает с предыдущей теоремой. Остается рассмотреть случай i¹j. Введем матрицу A¢, получающуюся из A заменой j -й строки на i -ю:
 .
.
Согласно свойству 3 определителей, будет  . С другой стороны, раскладывая, в соответствии с предыдущей теоремой, определитель A¢ по j -й строке, имеем:
. С другой стороны, раскладывая, в соответствии с предыдущей теоремой, определитель A¢ по j -й строке, имеем:  . Сравнивая правые части, получаем искомое. Теорема доказана.
. Сравнивая правые части, получаем искомое. Теорема доказана.
Применение определителей. Правило Крамера
Теорема Крамера. Пусть задана система линейных уравнений, содержащая n уравнений и n неизвестных:

| (*) |
Тогда, если определитель основной матрицы системы отличен от 0, система имеет единственное решение:

| (**), |
где
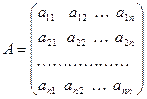 - основная матрица системы, D=detA,
- основная матрица системы, D=detA,  (k-ый столбец матрицы A заменен столбцом свободных членов).
(k-ый столбец матрицы A заменен столбцом свободных членов).
Доказательство.
Докажем сначала единственность решения. Домножим i -е уравнение системы на алгебраическое дополнение A ik и просуммируем получившиеся уравнения:


 .
.
Перегруппировав слагаемые и вынося за скобки xi: 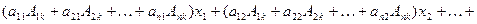
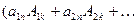
 ,
, 
Но  - разложение определителя по столбцу.
- разложение определителя по столбцу.
 ,
, 
По теореме из предыдущего раздела:
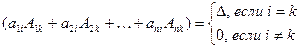 .
.
Получаем:  ,
,  .
.
Поскольку по предположению D¹0, то 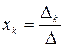 . Ввиду произвольности k получаем:
. Ввиду произвольности k получаем:  .
.
Таким образом, если вектор  служит решением системы (*), его координаты удовлетворяют формулам (**).
служит решением системы (*), его координаты удовлетворяют формулам (**).
Обратно, пусть координаты вектора  получены по формулам (**). Умножая матрицу A справа на столбец
получены по формулам (**). Умножая матрицу A справа на столбец  , получаем вектор-столбец S, k-я координата которого равна
, получаем вектор-столбец S, k-я координата которого равна 
т.е. столбец  .
.
Таким образом, вектор-столбец  служит решением матричного уравнения
служит решением матричного уравнения  . А это равносильно (см. пункт 3.3.) тому, что
. А это равносильно (см. пункт 3.3.) тому, что  - решение системы (*). Теорема доказана.
- решение системы (*). Теорема доказана.






