Вспомним решение одного линейного уравнения и системы из двух линейных уравнений с двумя неизвестными:
I. 
1) Если  ,
,  - единственное решение,
- единственное решение,
2) Если  ,
, 
a) 

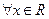 - бесконечное множество решений,
- бесконечное множество решений,
b) 

 - решений нет.
- решений нет.
II. 
1)  - единственное решение (графически: прямые пересекаются),
- единственное решение (графически: прямые пересекаются),
2)  - бесконечное множество решений (прямые совпадают),
- бесконечное множество решений (прямые совпадают),
3)  - Æ (решений нет) (прямые параллельны).
- Æ (решений нет) (прямые параллельны).
Определение. Система выражений вида

| (2.1) |
где 
 - коэффициенты при неизвестных, причем
- коэффициенты при неизвестных, причем  ,
,  ,
,  - неизвестные,
- неизвестные,  - свободные члены, называется системой линейных уравнений, состоящей из m уравнений с n неизвестными.
- свободные члены, называется системой линейных уравнений, состоящей из m уравнений с n неизвестными.
Определение. Коэффициенты при неизвестных системы (2.1) образуют прямоугольную таблицу чисел, которую будем называть матрицей данной системы:
 - основная матрица,
- основная матрица,
 - расширенная матрица.
- расширенная матрица.
Определение. Решениемсистемы (2.1) называется упорядоченная последовательность чисел 
 , если при подстановке чисел
, если при подстановке чисел  в систему (2.1) вместо неизвестных
в систему (2.1) вместо неизвестных  соответственно каждое из уравнений системы (2.1) обращается в верное равенство (тождество).
соответственно каждое из уравнений системы (2.1) обращается в верное равенство (тождество).

Определение. Если  то систему (2.1) будем называть однороднойсистемой линейных уравнений. Если
то систему (2.1) будем называть однороднойсистемой линейных уравнений. Если  то систему (2.1) будем называть неоднородной системой линейных уравнений.
то систему (2.1) будем называть неоднородной системой линейных уравнений.
Определение. Систему линейных уравнений будем называть совместной, если она имеет хотя бы одно решение. Если система (2.1) не имеет решений, то будем ее называть несовместной.
Определение. Совместную систему будем называть определенной, если она имеет одно решение. Если совместная система имеет более одного решения, будем называть неопределенной.
Рассмотрим систему линейных уравнений, состоящую из m уравнений с n неизвестными:
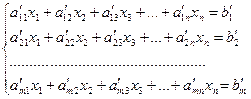
| 
|
Определение. Система линейных уравнений  называется следствием системы (2.1), если каждое решение системы (2.1) является решением системы
называется следствием системы (2.1), если каждое решение системы (2.1) является решением системы  .
.
Определение. Если обе системы (2.1) и  являются следствием друг друга, то они называются равносильными.
являются следствием друг друга, то они называются равносильными.
Под этим понимают, что они имеют одно и то же множество решений (возможно, пустое).
Теорема. Любая подсистема данной системы линейных уравнений является следствием данной системы.
Метод Гаусса
(метод последовательного исключения неизвестных)
Определение. Элементарными преобразованиями системы линейных уравнений называются:
1) перестановка местами уравнений;
2) умножение уравнения на любое число, отличное от нуля;
3) прибавления к уравнению другого уравнения;
4) приписывание (включение) в систему уравнения, которое является следствием данной системы;
5) исключение (вычеркивание) из системы уравнений, которые являются следствиями какой-либо подсистемы из остальных уравнений.
Теорема. При любом элементарном преобразовании система линейных уравнений обращается в систему, равносильную данной.
Пусть задана система, содержащая m линейных уравнений с n неизвестными:

| (2.1) |
Метод Гаусса заключается в последовательном исключении неизвестных.
Если среди уравнений системы (2.1) есть хотя бы одно уравнение вида 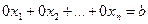 (*), где
(*), где  , то очевидно, что ни одна система значений
, то очевидно, что ни одна система значений  не удовлетворяет этому уравнению, а следовательно, и системе (2.1), поэтому система несовместна.
не удовлетворяет этому уравнению, а следовательно, и системе (2.1), поэтому система несовместна.
Пусть система (2.1) не содержит уравнений вида (*), значит в каждом уравнении системы хотя бы один коэффициент отличен от нуля.
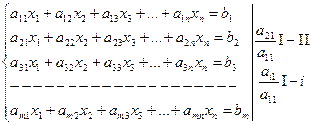 ,
,
где 
Оставив первое уравнение без изменения, исключим из всех уравнений системы (2.1), начиная со второго, неизвестную  .
.
I. Пусть  (в противном случае, применив элементарные строчечные преобразования, можно добиться, чтобы первый коэффициент первого уравнения был отличен от нуля)
(в противном случае, применив элементарные строчечные преобразования, можно добиться, чтобы первый коэффициент первого уравнения был отличен от нуля)

| (2.2) |
Перепишем систему

| ( ) )
|
 . Применяем те же рассуждения и исключаем из всех уравнений системы (
. Применяем те же рассуждения и исключаем из всех уравнений системы ( ), начиная с третьего, неизвестную
), начиная с третьего, неизвестную  .
.
II. Продолжая этот процесс, в результате получим систему:
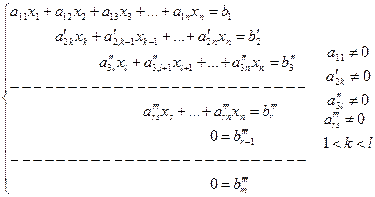
| (2.3) |
Система (2.3) имеет так называемый ступенчатый вид. Таким образом, доказана следующая теорема.
Теорема. Любая система линейных уравнений равносильна системе, имеющей ступенчатый вид.
Пример. Решить систему линейных уравнений методом Гаусса
1)





Система несовместна (решений нет).
2) Решить однородную систему линейных уравнений


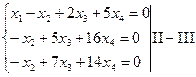
 - система, имеющая ступенчатый вид.
- система, имеющая ступенчатый вид.
Поскольку в ней количество неизвестных больше количества уравнений, ее решение заключается в том, чтобы выразить часть неизвестных (называемых главными) через другие неизвестные (называемые свободными). Так получается ее общее решение.
Определение. Общим решением линейных уравнений системы (2.1) называется решение, зависящее от параметров, такое что каждое решение данной системы получается из этого при соответствующем выборе значений параметров.
Определение. Решение системы, не зависящее от параметров, будем называть частным решением.
Пусть  - свободная неизвестная,
- свободная неизвестная,  - главные неизвестные.
- главные неизвестные.

 - общее решение данной системы. Записывая его в виде множества, имеем:
- общее решение данной системы. Записывая его в виде множества, имеем:  . Вынося общий множитель х 4, получаем другую форму записи общего решения:
. Вынося общий множитель х 4, получаем другую форму записи общего решения:  .
.






