Оглавление
Глава 1. Комплексные числа................................................. 5
1.1. Из истории возникновения................................................. 5
1.2. Определение комплексного числа...................................... 6
1.3. Действия над комплексными числами в алгебраической
форме................................................................................... 8
1.4. Свойства операций сложения и умножения...................... 9
1.5. Свойства операции сопряжения......................................... 10
1.6. Геометрическая интерпретация комплексного числа....... 11
1.7. Тригонометрическая форма комплексного числа............. 12
1.8. Действия над комплексными числами в тригонометрической форме 15
1.9. Возведение в степень комплексного числа в тригонометрической форме 16
1.10. Свойства модуля комплексного числа............................... 16
1.11. Извлечение корня из комплексного числа......................... 17
1.12. Показательная форма комплексного числа....................... 18
1.13. Другие арифметики для чисел а+bi................................... 19
Упражнения....................................................................................... 23
Глава 2. Системы линейных уравнений......................... 25
2.1. Общие сведения о системах линейных уравнений............ 25
2.2. Метод Гаусса (метод последовательного исключения
неизвестных)........................................................................ 27
2.3. Исследование системы линейных уравнений.................... 30
2.4. Арифметическое n-мерное векторное пространство.
Определение и свойства...................................................... 30
2.5. Линейная зависимость и линейная независимость конечной
системы векторов................................................................ 32
2.6. Ранг и базис конечной системы векторов.......................... 34
2.7. Ранг матрицы...................................................................... 36
2.8. Некоторые применения ранга матрицы............................ 38
2.9. Особенная и неособенная матрицы.................................... 40
2.10. Фундаментальная система решений однородной системы
линейных уравнений........................................................... 41
Упражнения....................................................................................... 43
Глава 3. Алгебра матриц........................................................... 46
3.1. Операции над матрицами................................................... 46
3.2. Обратная матрица.............................................................. 48
3.3. Матричный способ решения систем линейных
уравнений............................................................................ 49
Упражнения....................................................................................... 50
Глава 4. Определители.............................................................. 52
4.1. Определители 2-го и 3-го порядков................................... 52
4.2. Определители n-го порядка............................................... 53
4.3. Разложение определителя по строке (столбцу)................. 57
4.4. Применение определителей. Правило Крамера................ 59
4.5. Вычисление обратной матрицы......................................... 62
4.6. Вычисление ранга матрицы............................................... 62
4.7. Теорема Бине-Коши............................................................ 64
4.8. Теорема Лапласа................................................................. 64
Упражнения....................................................................................... 65
Варианты контрольных заданий......................................... 70
Литература....................................................................................... 72
Глава 1. Комплексные числа
Из истории возникновения
Комплексные числа, как, впрочем, и отрицательные, возникли из внутренней потребности самой математики, конкретнее – из практики и теории решения алгебраических уравнений. С комплексными числами впервые математики встретились при решении квадратных уравнений. Вплоть до ХVI века математики всего мира, не находя приемлемого толкования для комплексных корней, возникавших при решении квадратных уравнений, объявляли их ложными и не принимали во внимание.
История решения квадратных уравнений берет свое начало еще из Древнего Вавилона. Вавилоняне умели решать отдельные виды квадратных уравнений 2000 лет до н.э., правда, они находили только положительные корни и не владели общими методами решений. Индус Брахмагупта (II в.) изложил общее правило решения квадратного уравнения. Аль-Хорезми (IX в.) дал классификацию линейных и квадратных уравнений и привел способы их решений, правда, и он (как, впрочем, и все математики вплоть до XVII века) не принимал во внимание нулевые и отрицательные решения. Вывод формул решения квадратных уравнений в общем виде привел Виет (XVI в.). Однако и он признавал только положительные решения. Только в ХVI веке итальянские математики Тарталья, Кардано, Бомбелли учитывают, помимо положительных, отрицательные решения квадратных уравнений. Лишь в XVII веке, благодаря работам Жирара, Декарта, Ньютона и других математиков, решение квадратных уравнений приобретает современный вид.
Разрешимость уравнений 3-й и 4-й степеней была установлена названными выше итальянскими математиками Тарталья, Кардано и др., причем было установлено, что корни уравнений 3-й и 4-й степеней могут быть найдены с помощью формул, подобных формулам корней квадратных уравнений, но более сложных. Настойчивые поиски в течение почти двух столетий подобных формул для уравнений 5-й и более высоких степеней не увенчались успехом. Только в 20-х годах ХIX века молодой норвежский математик Нильс Абель доказал, что иррациональные корни алгебраических уравнений степени выше 4-й не могут быть выражены в виде формул, содержащих только пять операций – четырех арифметических и извлечения корней.
Кардано, занимавшийся решением уравнений 3-й и 4-й степеней (о чем речь шла выше), был одним из первых математиков, формально оперировавших комплексными числами, хотя их смысл во многом оставался для него неясным. Смысл комплексных чисел разъяснил другой итальянский математик Р.Бомбелли. В своей книге «Алгебра» (1572 г.) он впервые изложил правила действий над комплексными числами в современной форме. Большое внимание комплексным числам уделял А.Жирар, автор замечательного произведения «Новое изобретение в алгебре» (1629 г.). Именно А.Жирар впервые сформулировал основную теорему алгебры, впоследствии доказанную Гауссом. Вместе с тем, вплоть до XVIII века, комплексные числа считали «воображаемыми» и бесполезными. Интересно отметить, что даже такой выдающийся математик как Декарт, отождествлявший действительные числа с отрезками числовой прямой, считал, что для комплексных чисел не может быть никакого реального истолкования, и они навечно останутся воображаемыми, мнимыми. Аналогичных взглядов придерживались великие Ньютон и Лейбниц.
Лишь в XVIII веке многие задачи математического анализа, геометрии, механики требовали широкого применения операций над комплексными числами, что создало условия для разработки их геометрического истолкования.
Выдающаяся роль в развитии теории комплексных чисел, разработке методов их применения в различных областях математики принадлежит ряду известных математиков. В прикладных работах Даламбера и Эйлера в середине XVIII века авторы представляют произвольные мнимые величины в виде a+bi, что позволяет изображать такие величины точками координатной плоскости. Именно эта интерпретация была использована Гауссом в работе, посвященной исследованию решений алгебраического уравнения. Позднее, в начале ХIХ века в работах К.Весселя и Ж.Аргана содержится полное геометрическое построение комплексных чисел. В частности, Весселем комплексные числа рассматривались как векторы. Благодаря Коши в математике активно стали использоваться такие понятия, как модуль комплексного числа, сопряженные комплексные числа.
И только в начале XIX века, когда уже была выяснена роль комплексных чисел в различных областях математики, была разработана очень простая и естественная их геометрическая интерпретация, позволившая уяснить геометрический смысл операций над комплексными числами. Этому математика обязана Гауссу, опубликовавшему в 1831 г. свою работу по теории чисел. Тем самым был положен конец сомнениям в законном и полезном применении комплексного числа.
Определение комплексного числа
Мы знакомы с действительными числами. Рассмотрим теперь числа нового вида.
Определение. Числа вида z=a+bi, где a и b – действительные числа, i – мнимая единица, удовлетворяющая условию: i2=-1, будем называть комплексными.
Число a будем обозначать Rez и называть действительной частью комплексного числа z, bi – обозначать Imz и называть его мнимой частью, b – коэффициентом при мнимой части. Возможны случаи, когда действительные числа a и b могут быть равными нулю. Если a =0, то комплексное число bi называется чисто мнимым. Если b =0, то комплексное число a+bi равно a и называется действительным. Если a =0 и b =0 одновременно, то комплексное число 0+0 i равно нулю. Итак, мы получили, что действительные числа и чисто мнимые числа представляют собой частные случаи комплексного числа.
Запись комплексного числа в виде a+bi называется алгебраической формой комплексного числа.
Определение. Два комплексных числа a+bi и c+di условимся считать равными тогда и только тогда, когда в отдельности равны их действительные части и коэффициенты при мнимой единице, т. е.
a+bi=c+di, Û a=c и b=d
или

Пример. Найти x и y из равенства:
а) 3y+5xi=15-7 i;
б) (2x+3y)+(x-y) i=7+6i.
Решение. а) Согласно условию равенства комплексных чисел имеем 3y=15, 5x=-7. Отсюда 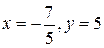 .
.
б) Из условия равенства комплексных чисел следует  .
.
Умножив второе уравнение на 3 и сложив результат с первым уравнением, имеем 5x=25, т. е. x =5. Подставим это значение во второе уравнение: 5-y=6, откуда y=-1. Итак, получаем ответ: x=5, y=-1.
Определение. Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью.
Если z=a+bi, тогда сопряженное ему число будет записано в виде:
 =a-bi.
=a-bi.
Рассмотрим степени мнимой единицы:
i1=i;
i 2=-1;
i 3= i 2× i =(–1)× i =- i;
i 4= i 3× i =- i × i =- i 2 =-(-1)=1;
i 5= i 4× i =1× i = i;
Если выписать все значения степеней числа i, то мы получим такую последовательность: i, -1, - i, 1, i, -1, - i, 1 и т. д. Легко видеть, что значения степеней числа i повторяются с периодом, равным 4.
Более точно, если показатель степени числа i делится на 4, то значение степени равно 1; если при делении показателя степени на 4 в остатке получается 1, то значение степени равно i; если при делении показателя степени на 4 получается остаток 2, то значение степени равно
-1; наконец, если при делении на 4 остаток равен 3, то значение степени равно - i. Пользуясь этим, можно вычислять любую степень числа i.
Пример. Найти: i28; i33; i135.
Решение. Имеем 28=4·7 (нет остатка); 33=4·8+1; 135=4·33+3.
Соответственно получим i28=1; i33=i; i135=-i.






