Определение. Рангом конечной системы векторов S называется максимальное число линейно независимых векторов данной системы.
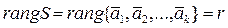
т.е.
1) 
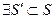, которая содержит r линейно независимых векторов.
2) Любая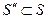 
, которая содержит больше чем r векторов, является линейно зависимой.
Свойства
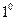
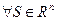
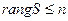
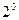
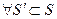
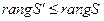
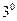
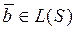Û 
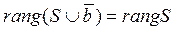
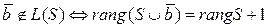
Определение. Элементарными преобразованиями системы векторов называются:
1) умножение какого-либо вектора системы на число, не равное нулю;
2) прибавление к какому-либо вектору системы другого вектора той же системы;
3) перестановка векторов местами;
4) вычеркивание (исключение) из системы вектора, являющегося линейной комбинацией остальных векторов системы;
5) приписывание к системе (ее пополнение) вектора, являющегося линейной комбинацией каких-либо векторов системы.
Определение. Подсистему данной конечной системы S будем называть базисом этой системы, если выполняются следующие условия:
1. 
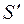- линейно независима
2. Каждый вектор системы S линейно выражается через систему .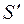
Свойства
Любая конечная система векторов S, содержащая хотя бы один ненулевой вектор, имеет базис.
Доказательство.
Пусть для определенности вектор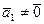 
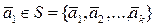. Тогда система 
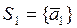- линейно независима.
Рассмотрим 2 возможные ситуации:
1. Каждый вектор системы S линейно выражается через систему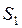 
, следовательно, система 
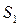-базис.
2. Некоторый вектор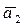 
нельзя линейно выразить через вектор 
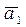, следовательно 
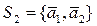- линейно независима.
Для системы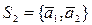 
рассмотрим 2 возможные ситуации:
а) Каждый вектор системы S линейно выражается через систему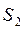 
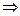система 
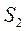- базис.
б)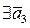 
, такой что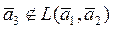 
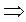
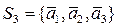- линейно независима и т.д.
Процесс выбора базиса завершится, так как S конечна. Свойство доказано.
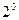Любые два базиса данной системы S имеют одинаковое число векторов.
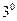Ранг данной системы векторов равен количеству векторов любого базиса данной системы.
Доказательство.
Пусть B – произвольный базис системы S. Тогда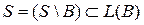 
.
Так как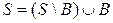 
, то по свойству 5) элементарных преобразований системы векторов 
.
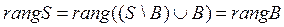Ранг матрицы
Определение. Напомним, что матрицей размера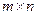 
(
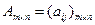) называется прямоугольная таблица чисел вида
.
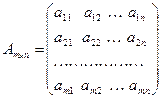В случае, когда значения m и n совпадают, матрицу будем называть квадратной матрицей порядка n:
.
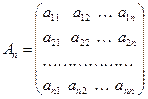Частным случаем матрицы размера 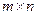является случай, когда одно из значений m или n равно 1: 
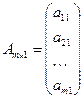или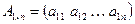 
, то есть матрица представляет из себя вектор-столбец или вектор-строку соответственно.
В общем случае каждая строка матрицы представляет собой n-мерный вектор, каждый столбец – m-мерный.
Транспонированной матрицей будем называть матрицу вида:
.
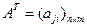Единичной матрицей будем называть квадратную матрицу вида: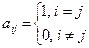 
, 
.
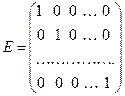Рассмотрим матрицы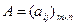 
и 
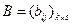. Матрицы A и B будем называть равными, если они одинакового размера, и равны их соответствующие элементы.
Определение. Элементарными строчечными (столбцовыми) преобразованиями матрицы являются:
1. умножение строки (столбца) на число отличное от нуля;
2. перестановка местами строк (столбцов);
3. прибавление одной (-ого) строки (столбца) к другой (-ому) строке (столбцу);
4. исключение строки (столбца), являющейся (являющегося) линейной комбинацией остальных строк (столбцов) матрицы;
5. включение строки (столбца), являющейся (являющегося) линейной комбинацией остальных строк (столбцов) матрицы.
Замечание. Если матрица A есть расширенная матрица некоторой системы линейных уравнений, то элементарные преобразования ее строк в точности соответствуют элементарным преобразованиям уравнений системы.
Определение. Строчечным (столбцовым) рангом матрицы A будем называть максимальное число линейно независимых вектор-строк (вектор-столбцов) матрицы.
Теорема. При любых элементарных строчечных преобразованиях матрицы строчечный и столбцовый ранги не меняются.
Теорема. Строчечный и столбцовый ранги матрицы равны.
Дано:
,
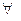
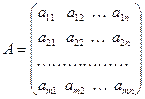
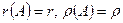где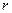 
и 
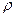- строчечный и столбцовый ранги.
Доказать: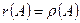 
.
Доказательство.
Приведем матрицу A с помощью элементарных строчечных преобразований к ступенчатому виду. Исключая из получившейся матрицы нулевые строки (если такие есть), получаем матрицу В.
~ 
.
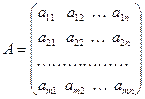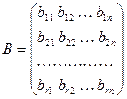Поскольку столбцы матрицы В являются векторами r-мерного пространства, получаем (с учетом предыдущей теоремы) последовательно:
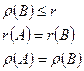(1)
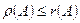(2)
Поскольку полученное неравенство справедливо для произвольной матрицы А, применяя те же рассуждения к АТ, получаем:
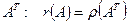
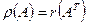
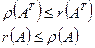(3)
На основе (2) и (3) можно сделать вывод о том, что: .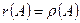
Следствие.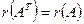 
.
Определение. Ступенчатой матрицей будем называть матрицу, удовлетворяющую следующим условиям:
1. если в i-ой строке матрицы первый ненулевой элемент стоит на k-ом месте, то в (i+1)-ой строке первые k элементов нули;
2. если i-ая строка – нулевая, то (i+1)-ая строка также нулевая.
Замечание. Именно к такому, т.е. ступенчатому, виду мы приводили расширенную матрицу системы линейных уравнений в методе Гаусса.
Теорема. Ранг ступенчатой матрицы равен числу ее ненулевых строк.
Доказательство.
Рассмотрим матрицу A порядка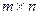 
, приведенную к ступенчатому виду:
(*)
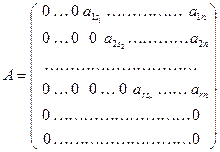
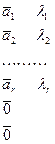
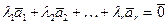Теорема доказана.
