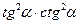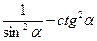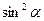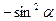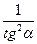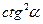1. Дописати співвідношення між тригонометричними функціями одного аргументу
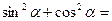


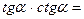


2. Самостійна робота (з подальшою перевіркою).
1) Установіть відповідність між поданими виразами та виразами, що їм тотожно дорівнюють (A – D)
| Варіант 1 | Варіант 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Відповідь:
|
Відповідь:
|
3. Знайдіть значення виразу: (можна користуватись довідковим матеріалом)
1) 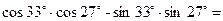 4)
4) 
2)  5)
5) 
3)  6)
6) 
4. Кожен ряд отримує завдання, представник групи виконує на дошці, потім група перевіряє.
Знайдіть значення виразу:
І ряд II ряд III ряд
 =
=  =
=  =
=
5. За допомогою формул перетворення суми тригонометричних функції в добуток (см. довідковий матеріал):
а) 
б) 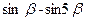
в) cos2 x + cos3 x
г) cos y – cos3 y
6. Учні працюють в парах. Спочатку кожен виконує свій варіант, потім обмінюються роботами і перевіряють за допомогою довідкового матеріалу.
Установіть відповідність між тригонометричними рівняннями (1-4) та їхніми розв’язками. (А-D)
| Варіант 1 | Варіант 2 |

| А | 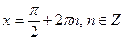
| |

| Б | 
| |

| В | 
| |

| Г | 
| |
| Д | 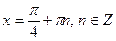
|
Відповідь:
| А | Б | В | Г | Д | |
| Х | |||||
| Х | |||||
| Х | |||||
| Х |

| А | 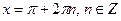
| |

| Б | 
| |

| В | 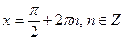
| |

| Г | 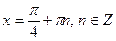
| |
| Д | 
|
Відповідь:
| А | Б | В | Г | Д | |
| Х | |||||
| Х | |||||
| Х | |||||
| Х |
7. Розв'язати найпростіші тригонометричні рівняння:
1) 
| 4) 
|
2) 
| 5) 
|
3) 
| 6)  
|
8. Дані рівняння розподілити по способах розв’язування тригонометричних рівнянь:
1. 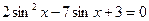
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
| Методи розв’язування рівнянь | Номер рівняння |
| Заміна змінних при розв’язуванні тригонометричних рівнянь | |
| Розв’язування тригонометричних рівнянь зведенням до однієї функції (з однаковим аргументом) | |
| Розв’язування однорідних тригонометричних рівнянь | |
| Зведення тригонометричного рівняння до однорідного | |
| Розв’язування тригонометричних рівнянь виду f(x) = 0 за допомогою розкладання на множники | |
| Відбір коренів тригонометричних рівнянь |
9. Розв'язати декілька рівнянь:
№1 
Розв'язання:




Тоді 
 ; або
; або 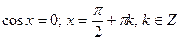 .
.
Враховуючи, що  , маємо
, маємо  и
и 
Відповідь:  ;
; 
№2 
Розв'язання:
 ,
,
 ,
,
 ,
,
нехай  ,
,  ,
,
 ,
,
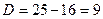 ,
,
 , ,
|  ; ;
|
 , ,
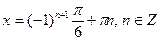 . .
| 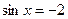 коренів немає, коренів немає,
|
Відповідь: 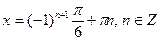 .
.
8. Показати розв’язання тригонометричної нерівності на одиничному колі:
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
ІІІ. Підсумки уроку
ІV. Домашнє завдання
Довідковий матеріал
І. Тригонометричні тотожності
| . Формули суми | 
|
| Формули переведення добутку в суму або різницю | 
|
| Основна тригонометрична тотожність та наслідки з неї | 
|
| Формули (теореми) додавання аргументів | 
|
| Формули подвійного аргументу | 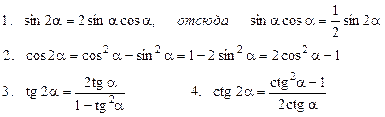
|
| Формули зниження степеня | 
|
ІІ. Тригонометричні рівняння та нерівності
1.Найпростіші тригонометричні рівняння

| 
| коренів немає |

| 
| |
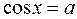
| 
| коренів немає |

| 
| |

| 
| 
|

| 
| 
|
Окремі випадки
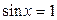 , , 
|  , , 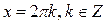
|
 , , 
|  , , 
|
 , , 
|  , , 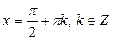
|
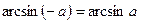
| 
|
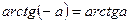
| 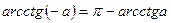
|
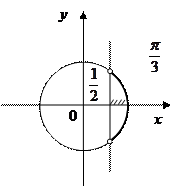
2.Приклади розв’язання найпростіших тригонометричних нерівностей
(за допомогою одиничного кола)
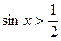
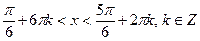
| 
|


| 

|


|   
|
Дидактичний матеріал
№1. Найдіть значення виразу:
1)  ; 3)
; 3)  ;
;
2)  ; 4)
; 4) 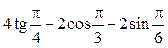 .
.
№2. Знайдіть значення тригонометричних функцій куту a, якщо відомо, що:
1)  ; 2)
; 2)  .
.
№3. Спростіть вираз:
1) 4cos23a + 4sin23a;
2) 1 – sin23 x;
3) tg 3b ctg 3b;
4) tg a cos a;
5) (1 – cos 3b)(1 + cos 3b).
6) 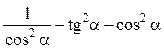 ;
;
7) cos4 x – sin4 x + sin2 x.
№4. Доведіть тотожність:
1)  ;
;
2)  .
.
№5. Обчисліть:
1) sin 17° cos 13° + cos 17° sin 13°;
2) sin 20° cos 50° – cos 20° sin 50°.
№6. Спростіть вираз:
1)  ;
;
2)  .
.
3)  ;
;
4)  ;
;
5)  .
.
№7. Обчисліть:а) sin 15°; б) cos 75°.
№8. Дано: 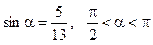 . Знайти sin 2a, cos 2a, tg 2a.
. Знайти sin 2a, cos 2a, tg 2a.
№9. Розв’язати рівняння:
1)  ; 4)
; 4)  ; 7)
; 7)  ;
;
2) 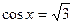 ; 5)
; 5)  ; 8)
; 8) 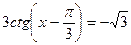 .
.
3) 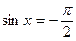 ; 6)
; 6)  ;
;
№10 Розв’язати рівняння:
1)  ;
;
2)  ;
;
3)  ;
;
4) 
5)  ;
;
6)  ;
;
7)  ;
;
8)  ;
;
9)  ;
;
10)  .
.
11) 
№11 Розв’язати рівняння:
1) 5cos2 x +7cos x -6 = 0; 7) 7sin2 x -2sin x = 0;
2) 5sin2 x -7cos x +1 = 0; 8) sin2 x +10cos2 x = 0;
3) 8tg2 x +10tg x +3 = 0; 9) 5cos2 x -14cos2 x +8 = 0;
4) cos x -2sin x = 0; 10) 3cos2 x -14cos x +7 = 0;
5) cos2 x +4cos x = 0; 11) 11sin2 x +6cos2 x +6 = 0;
6) sin3 x -sin7 x = 0; 12) 16cos x -11sin x -4 = 0.