1) знайти корені квадратного тричлена;
2) побудувати ескіз його графіка (параболу).
3) як відповідь записуються проміжки осі Ох, для яких точки параболи розміщені вище від осі Ох (
) і нижче від осі Ох (
).
( )
| ||
| 
| 
|
| 
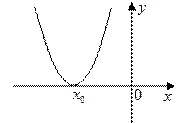
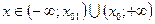
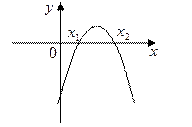
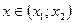
Розв’язків немає
| 
Розв’язків немає
|
4. Метод інтервалів
Означення Проміжки, на яких функція зберігає знак, називають проміжками знакосталості.
Якщо функція задана формулою 
, де 
– змінна, а 
– не рівні одне одному числа, то на кожному з проміжків, які визначаються нулями функції, ця функція зберігає знак, а при переході через нуль функції її знак змінюється.
Цю властивість використовують при розв’язуванні нерівностей методом інтервалів
Алгоритм розв’язування нерівностей методом інтервалів
1) знайти нулі функції ;
2) позначити на координатній прямій нулі функції;
3) встановить знаки функції на проміжках між нулями функції;
4) вибравши проміжки, на яких функція 
набуває значення відповідного знаку, записати множину розв’язків нерівності.
Дидактичний матеріал
№1. Розв’яжіть нерівність:
1) 
;
2) 
;
3) 
;
4) 
;
5) 
.
№2. Розв’яжіть нерівність:
1) 
;
2) 
;
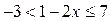3) 
;
4) 
;
5) 
.
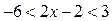№3. Розв’яжіть нерівність:
1) 
;
2) 
3) 
4) 
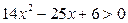
5) 
№4. Розв’яжіть нерівність:
1) 
;
2) 
;
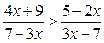3) 
;
4) 
;
5) 
.
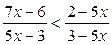№5. Розв’яжіть нерівність:
1) 
;
2) 
>0;
3) 
;
4) 
;
5) 
.
№6. Знайдіть область визначення функції:
1) 
;
2) 
;
3) 
;
4) 
;
5) 
.
№7. Для кожної системи нерівностей укажіть множину її розв’язків:
1) 
2) 
3) 
4) 
5) 
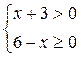6) 
№8 Для кожної нерівності укажіть множину його розв’язків:
а) 
;
б) 
;
в) 
;
г)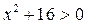 
;
д) 
;
е)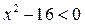 
.
№9. Яка кількість цілих чисел є розв’язками системи нерівностей 
№10 Знайдіть найбільше ціле число, що є розв’язком системи нерівностей
№11 Знайдіть найменше ціле число, що є розв’язком системи нерівностей
 |
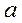№12. Знайдіть всі значення параметра, при яких сума коренів рівняння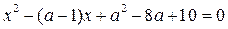 
більше від 4, а добуток менше від 3.
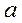
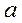№13. Знайдіть всі значення параметра, при яких нерівність 
має хоча б один розв’язок.
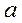№14. Знайдіть всі значення параметра, при яких нерівність 
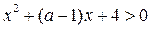виконується при будь-яких значеннях змінної.
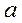№15. Знайдіть всі значення параметра, при яких нерівність 
не має розв’язків.
Урок 5
Тема. тригонометричнІ тотожностІ, основнІ способИ розв’язання тригонометричних рівнянь.
Мета. Узагальнити та систематизувати знання учнів із тем «Перетворення тригонометричних виразів» «Тригонометричні рівняння та нерівності»;
удосконалювати вміння та навички учнів перетворювати тригонометричні вирази та рівняння та нерівності.
Хід уроку
І. Організаційний етап уроку
ІІ. Формулювання теми, мети та задач уроку; мотивація навчальної діяльності.
