Мета. Узагальнити і систематизувати знання про нерівності (поняття нерівності,
властивості нерівностей, алгоритм розв’язування нерівностей, нерівності з модулем);
розвивати навички самостійної роботи, уміння обґрунтовувати дії, що виконуються, інтерес до предмету, розширювати загальний кругозор учнів;
виховувати свідоме ставлення до навчання, пізнавальну активність, почуття особистої відповідальності за колективну роботу.
Тип уроку. Урок узагальнення та систематизації знань.
Обладнання. Мультимедійний проектор, екран, навчальна презентація.
Хід уроку
І. Організаційний момент.
ІІ. Перевірка домашньої роботи.
ІІІ. Узагальнення та систематизація знань.
Повторюємо відомості про нерівності за допомогою презентацій, які підготовили учні до уроку.
Слайд 1 «Лінійні нерівності»
· Що називають розв’язком нерівності з однією змінною?
· Що означає розв’язати нерівність?
· Які нерівності називаються рівносильними?
· На основі яких властивостей виконується заміна нерівності на рівносильну їй нерівність?
Приклади:
1) 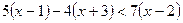 , 2)
, 2)  ,
,
 ,
,  ,
,
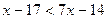 ,
,  ,
,
 ,
,  ,
,
 , розв’язком нерівності буде
, розв’язком нерівності буде
 ,
,  . будь-яке число,
. будь-яке число,  .
.
Відповідь.  . Відповідь.
. Відповідь.  .
.
3)  ,
,
 ,
,
 ,
,
 ,
,
 , нерівність не має розв’язків.
, нерівність не має розв’язків.
Відповідь. Розв’язків нема.
Учні самостійно виконують
№1 Розв’язати нерівності:
1)  ;
;
2)  .
.
Перевіряємо відповіді.
Слайд 2 «Квадратні нерівності»
· Які нерівності називають нерівностями другого степеня з однією змінною?
· Як розв’язати нерівності:
 ,
,  ,
,  ,
,  , де
, де  ?
?
· В чому полягає алгоритм розв’язування нерівності  ,
,  ,
,  ,
,  , де
, де  , в залежності від
, в залежності від  та
та  ?
?
Приклади
Розв’яжіть нерівності:
1)  , 2)
, 2)  ,
,
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
 |  |
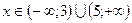 .
.  .
.
Відповідь. 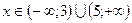 . Відповідь.
. Відповідь.  .
.
3)  , 4)
, 4) 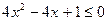

 ,
,  ,
,  ,
,  ,
,
 |
 .
.
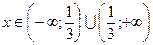 . Відповідь.
. Відповідь.  .
.
Відповідь. 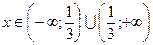 .
.
Слайд 3 «Дробно-раціональні нерівності»
· На яку властивість функції спирається метод інтервалів?
· Алгоритм розв’язування нерівностей методом інтервалів.
Приклади
Розв’яжіть нерівності:
1)  , 2)
, 2)  ,
,
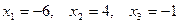 ,
,  ,
,  ,
,
 |  |
 .
. 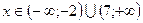 .
.
Відповідь.  . Відповідь.
. Відповідь. 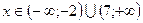 .
.
3)  ,
,

 ,
,
 ,
,  ,
,  ;
;
 ,
,  ;
;
 .
.
Відповідь.  .
.
Слайд 4 «Нерівності, що містять змінну під знаком модуля»
·Алгебраїчне та геометричне означення модуля, властивості модуля.
·Алгоритм розв’язування нерівностей, що містять змінну під знаком модуля.
Приклади
Розв’яжіть нерівності:
1)  , 2)
, 2)  ,
,
 , за властивістю модуль приймає
, за властивістю модуль приймає
 , лише невід’ємні значення, тому
, лише невід’ємні значення, тому
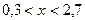 . дана нерівність не має розв’язків.
. дана нерівність не має розв’язків.
Відповідь.  . Відповідь. Розв’язків не має.
. Відповідь. Розв’язків не має.
3)  , 4)
, 4)  ,
,
за властивістю модуль приймає  або
або  ,
,
додатні значення тоді, коли не  ,
,  ,
,
дорівнює нулю, отже  ,
,  ,
,  .
.
 .
. 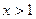 .
.
Відповідь.  . Відповідь.
. Відповідь. 






