Мета. Повторити, узагальнити й систематизувати знання учнiв про
арифметичний корiнь n-го степеня, степiнь iз рацiональним показником
та їxнi властивостi, формувати вмiння застосовувати їx для перетворення
виразiв.
Учнi повиннi: умiти перетворювати та обчислювати вирази, що мiстять:
а) коренi n-го степеня;
б) степiнь iз рацiональним показником.
Обладнання: роздавальний матерiал (роздруки таблиць «Означення»,
«Властивостi коренiв n-го степеня», «Властивостi степеня з
рацiональним показником»).
Тип уроку: повторення, узагальнення й систематизацiї знань учнiв.
Хiд уроку
I. Органiзацiйний етап.
II. Перевiрка домашнього завдання.
III. Актуалiзацiя опорних знань учнiв.
Вiдповiдi на питання:
● Закiнчiть речення «Коренем n-го степеня з числа  називається таке число, …».
називається таке число, …».
● Чому дорiвнює  ?
?
● Чи iснує корiнь парного степеня з вiд`ємного дiйсного числа?
● Закiнчiть речення «Арифметичним коренем n-го степеня з невiд`ємного числа  називається…» (скористатися таблицею «Означення»).
називається…» (скористатися таблицею «Означення»).
● Чому дорiвнює  )n, якщо х
)n, якщо х 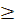 0?
0?
● Чому дорiвнює 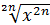 , n
, n  1- натуральне число?
1- натуральне число?
● Знайдiть значення виразу  .
.
● Обчислiть  .
.
● Чому дорiвнює добуток  ·
· 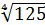 ?
?
● Знайдiть значення частки 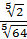 . (скористатися таблицею «Властивостi коренiв n-го степеня»).
. (скористатися таблицею «Властивостi коренiв n-го степеня»).
● Дайте означення степеня з натуральним показником.
● Дайте означення степеня з цiлим вiд`ємним показником, з нульовим показником.
● Дайте означення степеня з рацiональним показником.
● Чим вiдрiзняються областi допустимих значень виразiв:  n, де n
n, де n 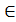 N;
N;  -n, де n
-n, де n 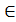 N;
N;  ґ, де ґ =
ґ, де ґ =  ?
?
● При яких  iснує
iснує  n (скористатися таблицею «Означення»).
n (скористатися таблицею «Означення»).
● Сформулюйте властивостi степеня з рацiональним показником (скористатися таблицею «Властивостi степеня з рацiональним показником»).
IV. Формування вмінь.
Завдання високого рiвня розбираються бiля дошки, а достатнього коментуються учнями з мiсця.
1. Знайдiть значення виразу  ·
·  .
.
Розв`язання
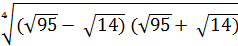 =
=  =
= 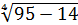 =
=  = 3.
= 3.
Вiдповiдь: 3.
2. Звiльнiться вiд iррацiональностi в знаменнику дробу  .
.
Розв`язання
 =
=  =
= 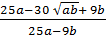 .
.
Вiдповiдь: 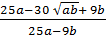 .
.
3. Винесiть множник з-пiд знака радикала 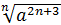 .
.
Розв`язання
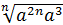 =
=  =
=  2
2  .
.
Вiдповiдь:  2
2  .
.
4. Внесiть множник пiд знак радикала ( +b)
+b) 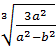 .
.
Розв`язання
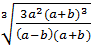 =
=  .
.
Вiдповiдь: 
5. Спростiть вираз  .
.
Розв`язання
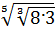 =
=  .
.
Вiдповiдь:  .
.
6. Порiвняйте  i
i 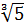 .
.
Розв`язання
 =
=  =
=  ,
, 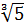 =
=  =
=  .
.
 . Отже,
. Отже,  <
< 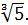
Вiдповiдь:  <
< 
7. Обчислiть 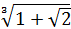 ·
· 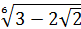 .
.
Розв`язання
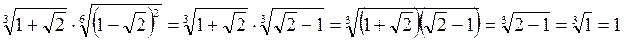
Вiдповiдь: 1.
8. Знайдiть значення виразу  , якщо x = 3,5.
, якщо x = 3,5.
Розв`язання
 =
= 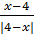 .
.
Оскiльки х = 3,5, то 4-х>0, тодi |4-x| = 4-x.
 =
= 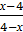 = -1.
= -1.
Вiдповiдь: -1.
9. Спростiть вираз  .
.
Розв`язання
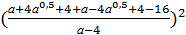 = (
= ( = 22 = 4.
= 22 = 4.
Вiдповiдь: 4.
10.Знайдiть значення виразу 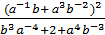 , якщо а=-10, b=2.
, якщо а=-10, b=2.
Розв`язання
 =
= 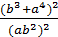 :
:  =
= 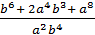 ·
· 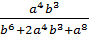 =
=  .
.
Якщо  = -10, b = 2, то
= -10, b = 2, то 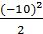 =
=  = 50.
= 50.
Вiдповiдь: 50.
V. Пiдведення пiдсумкiв уроку.
Учитель звертає увагу учнiв на головне на даному уроцi i вiдповiдає на запитання учнiв.
VI. Домашнє завдання.
1. Знайдiть значення виразу:
а)  ; б)
; б) 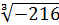 + 4(
+ 4( )6 – 3
)6 – 3  ;
;
в) (2 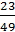 ) -1,5; г)
) -1,5; г)  · 491,25.
· 491,25.
2. Звiльнiться вiд iррацiональностi в знаменнику дробу:
а)  ; б)
; б) 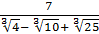 .
.
3. При яких значеннях змiнної х не має змiсту вираз:
а)  ; б)
; б) 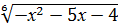 ?
?
4. Знайдiть область допустимих значень виразу:
а)  ; б) (х2 – 4)0.
; б) (х2 – 4)0.
Довідковий матеріал
Означення
| Означення | Приклади |
Корiнь n-го степеня з числа  – це таке число, n-й степiнь якого дорiвнює числу – це таке число, n-й степiнь якого дорiвнює числу  (n є N). (n є N).  – корiнь, n – показник, – корiнь, n – показник,  – пiдкореневий вираз. – пiдкореневий вираз.
|  = 5, 54 = 625; = 5, 54 = 625;
 = -7, (-7)3 = -343. = -7, (-7)3 = -343.
|
Арифметичним коренем n-го степеня з невiд`ємного числа називається таке число 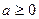 , n-й степiнь якого дорiвнює , n-й степiнь якого дорiвнює  . .
|  = 2 – арифметичний корiнь. = 2 – арифметичний корiнь.
|
| Показники коренiв вигляду n=2k+1 використовують для позначення будь-яких коренiв; показники вигляду n=2k – тiльки для позначення арифметичних коренiв. n є N, але n ≠ 1. | 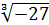 = -3; = -3;
 = 8. = 8.
|
Степенем числа  >0 з рацiональним показником r = >0 з рацiональним показником r =  , де m – цiле, а n>1 – натуральне число, називають число , де m – цiле, а n>1 – натуральне число, називають число  , тобто , тобто  = =  . .
| 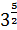 = =  = 9 = 9  ; ;
 = = 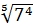 . .
|
Властивості кореня
| Властивостi коренiв n-го степеня | Приклади |
(n є N, n≠1):
1.  = 0
2. = 0
2.  = 1
3. = 1
3.  , ,  ≥0, b≥0
4.. ≥0, b≥0
4..  ≥0, b≥0
5. ≥0, b≥0
5.  = = 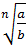 , ,  ≥0, b>0
6. ≥0, b>0
6. 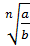 = =  , ,  ≥0, b>0
7. ( ≥0, b>0
7. ( )k = )k = 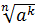 , ,  >0, kєZ
(якщо kєN, то рiвнiсть справджується й тоді, коли >0, kєZ
(якщо kєN, то рiвнiсть справджується й тоді, коли  =0)
8. =0)
8.  = = 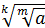 = = 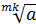 , ,  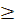 0, m є N, k є N, m≠1, k≠1
9. 0, m є N, k є N, m≠1, k≠1
9.  = =  , m є N, q є N, m≠1. , m є N, q є N, m≠1.
|
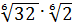 = =  = 2 = 2
 = =  · ·  = 3·2 = 6 = 3·2 = 6

 = =  = =  (2
(2  = 23 = 23  = 8 · 0,3 = 2,4 = 8 · 0,3 = 2,4
 = = 
 = = 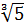
|
2. Властивості степеня
Властивостi степеня з рацiональним показником ( >0, b>0, r, s – рацiональнi числа) >0, b>0, r, s – рацiональнi числа)
| Приклади |
1.  r · r ·  s = s =  r+s
2. r+s
2.  = =  3. (
3. ( r)s = r)s =  rs
4. ( rs
4. ( b)r = b)r =  r br
5. r br
5.  )r = )r = 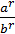 6.
6.  r > 0
7. r > 0
7.  r > 1, якщо r > 1, якщо  >1, r>0; >1, r>0;
 r < 1, якщо r < 1, якщо  >1, r<0.
8. >1, r<0.
8.  r > r >  s, якщо s, якщо  >1, r>s; >1, r>s;
 r < r <  s, якщо 0< s, якщо 0<  <1, r>s
9. <1, r>s
9.  r < br, якщо r>0, r < br, якщо r>0,  <b; <b;
 r > br, якщо r<0, r > br, якщо r<0,  <b <b
|  · · 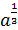 = = 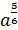
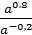 = = 
 = 2-1 = = 2-1 = 
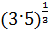 = =  · ·  (
( -0,4 = -0,4 = 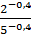 = 2,50,4 = 2,50,4
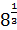 = ( = (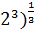 = 2>0 = 2>0
 = (22 = (22  = 2>1 = 2>1
 = (53 = (53  = 5-1 = = 5-1 =  <1 <1
 > > 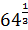 , 8>4
( , 8>4
(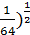 < ( < (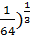 , ,  < < 
 < <  , ,  <5 <5
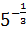 > >  , , 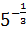 > 5-1 > 5-1
|
Дидактичний матеріал
Завдання основного рiвня
Спростiть вираз:
№1. а) 6 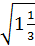 -
- 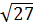 ; б) 15
; б) 15  ;
;
А) -  ; Б)
; Б)  ; А)
; А) 
В) 1; Г) iнша вiдповiдь. 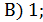 Г) iнша вiдповiдь.
Г) iнша вiдповiдь.
№2. а)  +
+ 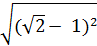 ; б)
; б) 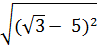 +
+  ;
;
А) 1; Б) 3; В) -2  ; Г) iнша вiдповiдь. А) 4; Б) 6; В) -2
; Г) iнша вiдповiдь. А) 4; Б) 6; В) -2  ; Г) iнша вiдповiдь.
; Г) iнша вiдповiдь.
№3. а) 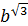 (
( ; б)
; б) 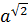 (
(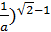 .
.
А) –b; Б) b; В) 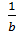 ; Г) iнша вiдповiдь. А)
; Г) iнша вiдповiдь. А) 
 ; Г) iнша вiдповiдь.
; Г) iнша вiдповiдь.
Обчислiть:
№4. а) ( ; б) (
; б) ( ;
;
А) 3  ; Б)
; Б)  ; В)
; В)  ; Г) iнша вiдповiдь. А) 81; Б) 135; В)
; Г) iнша вiдповiдь. А) 81; Б) 135; В)  ; Г) iнша вiдповiдь.
; Г) iнша вiдповiдь.
№5. а) ( б) (
б) ( +
+  ;
;
А) 22; Б) 6; В) 11; Г) iнша вiдповiдь. А) 3; Б) 8; В) 6; Г) iнша вiдповiдь.
№6. а) 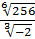 ; б)
; б)  .
.
А) 2; Б)  ; В) -2; Г) iнша вiдповiдь. А) -3; Б) -1; В)
; В) -2; Г) iнша вiдповiдь. А) -3; Б) -1; В)  ; Г) iнша вiдповiдь.
; Г) iнша вiдповiдь.
Звiльнiться вiд iррацiональностi в знаменнику дробу:
№7. а) 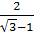 ; б)
; б) 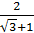 ;
;
А) 2(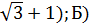 2
2 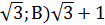 ; А) 2(
; А) 2(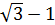 ); Б) 2
); Б) 2  ; В)
; В) 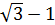 ;
;
Г) iнша вiдповiдь. Г) iнша вiдповiдь.
№8. а) 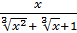 ; б)
; б)  .
.
А)  -1; Б)
-1; Б) 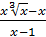 ; В) 1; А)
; В) 1; А) 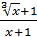 ; Б)
; Б)  ; В) 1; Г) iнша вiдповiдь.
; В) 1; Г) iнша вiдповiдь.
Г) iнша вiдповiдь.
Винесiть множник з-пiд знака радикала:
№9. а) 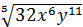 ; б)
; б)  ;
;
А) 2xy 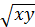 ; Б) 2ху2
; Б) 2ху2  ; А) -4
; А) -4  y
y 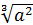 ; Б) 4
; Б) 4  2y
2y 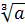 ; В) -4
; В) -4  y
y 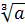 ;
;
В) 2ху  ; Г) iнша вiдповiдь. Г) iнша вiдповiдь.
; Г) iнша вiдповiдь. Г) iнша вiдповiдь.
№10. а) 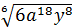 , якщо a>0, y>0; б)
, якщо a>0, y>0; б)  , якщо x>0, y>0.
, якщо x>0, y>0.
А)  3у
3у  ; Б)
; Б)  3y|
3y|  ; А) 2х2 |y|
; А) 2х2 |y|  ; Б) 2х2у
; Б) 2х2у  ;
;
В)  3у
3у 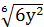 ; Г) iнша вiдповiдь. В) 2|х2у|
; Г) iнша вiдповiдь. В) 2|х2у|  Г) iнша вiдповiдь.
Г) iнша вiдповiдь.
Внесiть множник пiд знак радикала:
№11. а) 3ху3  , якщо x>0, y>0; б) 4xy
, якщо x>0, y>0; б) 4xy  , якщо х>0, y>0;
, якщо х>0, y>0;
А)  ; Б)
; Б)  ; А)
; А)  ; Б)
; Б)  ; В) -
; В) - 
В) -  ; Г) iнша вiдповiдь. Г) iнша вiдповiдь.
; Г) iнша вiдповiдь. Г) iнша вiдповiдь.






