Учитывая, что p = nkT, а следовательно p 0 = n 0 kT, от формулы
| (10.2.7) придем к формуле для концентраций частиц | ||||
| n = n | exp | − m 0 gh . | (10.3.1) | |
| kT |
Так как молекулы воздуха находятся в поле тяготения Земли, то на разной высоте молекулы обладают различным запасом потенциальной энергии П = m 0 gh. Следовательно, распределение молекул по высоте яв-ляется и распределением молекул по значениям потенциальной энергии
| П | ||||||
| n = n 0exp | − | , | (10.3.2) | |||
| kT |
где n 0 − концентрация молекул в том месте, где потенциальная энер-гия молекул равна нулю.
Больцман доказал, что распределение (10.3.2) справедливо не толь-ко в случае поля тяготения Земли, но и в любом потенциальном поле сил для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения. В соответствии с этим выражение
(10.3.2) получило название распределение Больцмана.
Например, для частиц находящихся в поле центробежных сил
П = − m 0ω2 r 2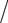 
2 (где r − расстояние от оси вращения до частицы). То-гда выражение (10.3.2) примет вид
| m | ω2 r 2 | (10.3.3) | |||
| n = n 0exp | 0 | . | |||
| 2 kT | |||||
Для частиц, взвешенных в жидкости (частицы суспензии или эмульсии), в выражении для потенциальной энергии необходимо учи-тывать действие силы Архимеда. Поэтому потенциальная энергия та-
ких частиц будет иметь вид:
| в поле силы тяжести | ||||||||||
| П = (m 0 − m ж) gh = (ρ 0 −ρж) Vgh, | (10.3.4) | |||||||||
| в поле центробежных сил | ||||||||||
| П = − (m − m | ) ω2 r 2 | = − (ρ | −ρ | ж | ) V ω2 r 2 | , | (10.3.5) | |||
| ж | ||||||||||
где m ж − масса жидкости, вытесненной частицей массой m 0; ρ0 − плотность вещества частиц; ρж − плотность жидкости; V − объем час-тицы.
Распределение Больцмана для частиц суспензии или эмульсии будет иметь вид:
поле силы тяжести
| n = n | exp | − ( m 0 | − m ж ) gh | = n | exp | − (ρ 0 | −ρ ж ) Vgh | . (10.3.6) | |||||
| kT | kT | ||||||||||||
в поле центробежных сил
| (m | − m )ω2 r 2 | (ρ | −ρ | ж | ) V ω2 r 2 | . (10.3.7) | ||||||
| n = n 0exp | ж | = n 0 exp | ||||||||||
| 2 kT | 2 kT |
Для идеального газа в любом внешнем потенциальном поле рас-пределение молекул будет подчиняться распределению Больцманом. В общем случае функция распределения Больцмана будет иметь вид
| f (x, y, z)= A exp | − | П(x, y, z ) | , | (10.3.8) | |
| kT |
где П(х, у, z) − потенциальная энергия молекулы в точке с координа-тами х, у, z; A − нормировочная постоянная.
Общее распределение молекул идеального газа во внешнем поле по их значениям проекций скоростей и координат х, у, z имеет вид
| f (ε)= B exp− | ε | , | |||||||||||
| kT | |||||||||||||
| − функция распределения Максвелла − Больцмана, | |||||||||||||
| m | υ 2 | m 0υ2 y | m | υ 2 | + П(x, y, z) = | m | υ2 | + П(x, y, z) | |||||
| где ε = | x | + | + | z | |||||||||
энергия молекулы; В − нормировочная постоянная.
(10.3.9)
− полная
