После решения системы канонических уравнений (4.6) и определения реакций лишних связей X 1, X 2, …, Xn внутренние усилия можно найти как в любой статически определимой системе, загруженной заданной нагрузкой и найденными реакциями этих связей. Однако, учитывая, что в процессе решения задачи мы построили эпюры `M 10, `M 20,…, `Mn 0 – от единичных значений неизвестных и эпюру Mp 0 – от заданной нагрузки, удобнее воспользоваться принципом суперпозиции и вычислить эти внутренние усилия по формулам:
Mp = Mp 0 + S `Mi 0 Xi;
Qp = Qp 0 + S `Qi 0 Xi; (4.7)
Np = Np 0 + S `Ni 0 Xi,
где Mp, Qp, Np – соответствующие усилия в заданной СНС от заданной нагрузки; Mp 0, Qp 0, Np 0– те же усилия в ОС МС от заданной нагрузки; `Mi 0, `Qi 0, `Ni 0 – эти же усилия в ОС МС от Xi = 1.
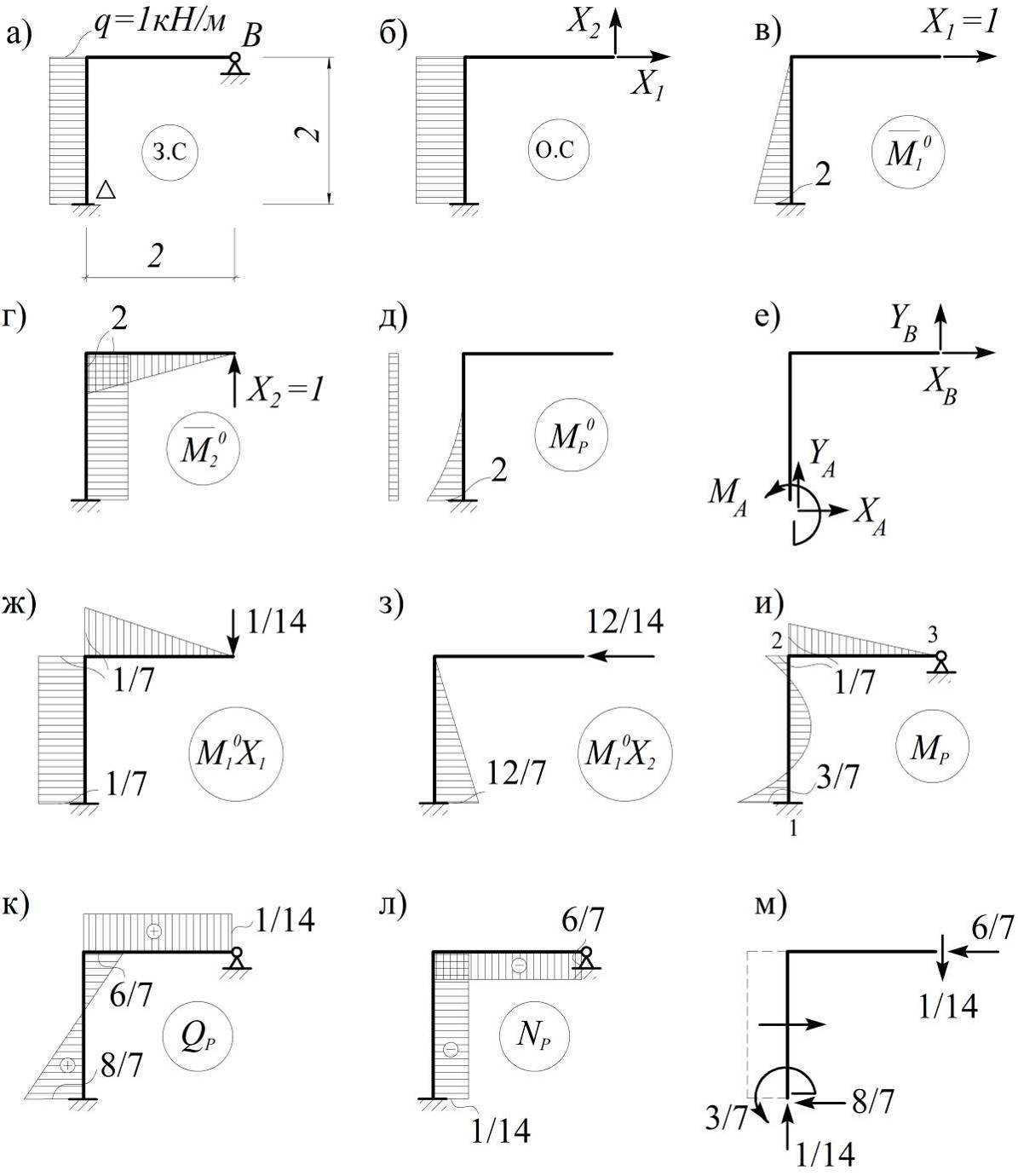
Рис. 4.5
Поскольку при расчете рам учитываются только изгибные деформации, которым соответствуют изгибающие моменты, по формулам (4.7) определяют лишь первое из внутренних усилий – Mp. Эпюру Qp удобнее построить по эпюре Mp, используя дифференциальную зависимость Qp = dMp / dx, а эпюру Np – по эпюре Qp, рассматривая равновесие вырезанных узлов рамы.
Рассмотрим такую процедуру на примере фрагмента рамы, приведенного на рис. 4.6, а.
Пусть на вертикально расположенных участках k - i и j - l эпюра Mp линейна и знакопостоянна, а на горизонтальном участке i - j, загруженном равномерно распределенной нагрузкой, представляет собой параболу.
Очевидно, что на последнем участке рамы эпюра Mp не отличается от эпюры моментов в простой двухопорной балке соответствующего пролета, загруженной равномерно распределенной нагрузкой и концевыми моментами (рис. 4.6, б), и ее в общем случае можно представить в виде суммы:
Mp (x) = Mp 0 (x) + Mp к(x), (4.8)
где Mp 0 (x) – эпюра от собственной нагрузки внутри пролета, а Mp к(x) – эпюра от концевых моментов, показанная пунктиром на рис. 4.6, в.
| l |

Рис. 4.6
Дифференцируя (4.8), и рассматривая полученное выражение на концах участка, получим:
Qij = Qij 0 + (M пр – M лев)/ lij, (4.9)
где Qij и Qij 0 – поперечные силы от заданной и от местной нагрузки в i -м узле рамы на участке i - j (рис. 4.6, г – д), а М пр и М лев – значения моментов на концах соответствующей балки, взятые с учетом знаков из сопромата. Аналогично под Qji будем понимать поперечную силу в j -ом узле этого участка. Тогда в нашем примере М пр = – Mj, а М лев = – Mi, поэтому
Qij = ql /2 + (Mi – Mj)/ lij;
Qji = – ql /2 + (Mi – Mj)/ lij.
Применяя соответствующие обозначения для продольных сил и рассматривая равновесие i -го узла рамы, получим (рис. 4.6, е):
S X = 0; _ Nij = – Qik;
S Y = 0; _ Nik = – Qij.
Аналогичные уравнения, получаемые из условия равновесия рассматриваемого j -го узла рамы или ригеля i - j в целом, можно использовать для проверки найденных результатов.
Вернемся теперь к рассмотрению рамы на рис. 4.5, а.
Пример 4.3. Построить эпюры внутренних усилий для заданной рамы (рис. 4.5, а).
Решение.
1. Находим изгибающие моменты по формуле (4.7):
Mp = Mp 0 + `M 10 X 1 + `M 20 X 2,
воспользовавшись найденными ранее значениями X 1 и X 2 – см. пример 4.2.
На ригеле эта эпюра совпадает с эпюрой `M 10 X 1 (рис. 4.5, ж), поскольку на этом участке эпюры Mp 0 и `M 20 равны нулю. Для построения Mp на стойке достаточно вычислить ее значения в 1-м узле (рис. 4.5, и): M 1 = 2 + (1/7) – (12/7) = 3/7кНм.
2. При построении эпюры на стойке будем для определенности считать первый узел – левым, а второй – правым. Тогда по формуле (4.9) получим:
Q 12 = ql 12/2 + (M пр – M лев)/ l 12 = (1×2)/2 + [(–1/7) – (–3/7)]/2 = 1 + 1/7 = 8/7;
Q 21 = - ql 12/2 + (M пр – M лев)/ l 12 = - 1 + 1/7 = - 6/7кН.
На ригеле местная нагрузка отсутствует, поэтому (рис. 4.5, к):
Q 23 = Q 32 = (1/7)/2 = 1/14кН.
3. Для построения эпюры Np достаточно рассмотреть равновесие 2-го узла рамы:
S X = 0; _ N 23 = – Q 21 = – 6/7 кН;
S Y = 0; _ N 21 = – Q 23 = – 1/14 кН.
Для проверки правильности построения эпюр можно рассмотреть равновесие части рамы (рис. 4.5, м), расположенной выше сечения, проведенного вблизи опор A и B,где известны значения всех трех эпюр:
S X = 2 – 6/7 – 8/7 = 0;
S Y = 2/7 – 2/7 = 0;
S MA = 3/7 – 2×1 + (6/7)×2 – (1/14) ×2 = 0. ·






