Теорема 3.2. (Об эквивалентности пар на плоскости). Две пары, лежащие в одной плоскости и имеющие равные по величине и по знаку моменты, эквивалентны.
Для доказательства рассмотрим две пары (Р, Р ¢) и (F, F ¢), лежащие в одной плоскости и имеющие равные по величине и по знаку моменты (Рис.3.4).
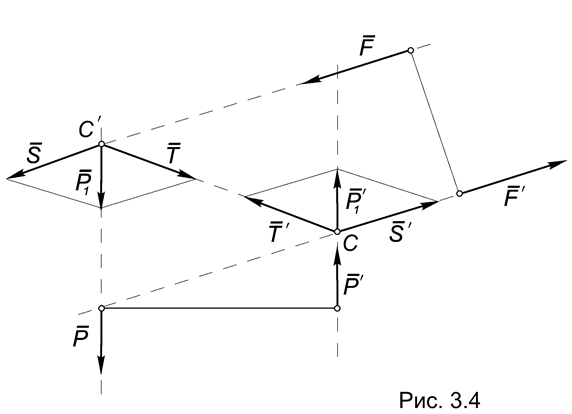
Продолжим линии действия сил пар до их пересечения в точках С и С ¢.
На основании следствия из аксиомы 3 действие сил Р и Р ¢ не изменится, если эти силы перенести в эти точки, то есть (Р, Р ¢) ~ (Р 1, Р 1 ¢).
Воспользовавшись аксиомой 4, заменим силу Р 1составляющими S и T, направленными, соответственно, вдоль линии действия силы F, и по прямой СС ¢. Аналогично поступим с силой Р 1 ¢, заменив ее составляющими S¢ и T¢.
По построению T = - T¢, поэтому согласно аксиоме 2: (T, T¢) ~ 0 и в соответствии с аксиомой 3 эту систему можно исключить.
Таким образом,
(Р, Р ¢) ~ (Р 1, Р 1 ¢) ~ ((S, T),(S¢, T¢)) ~ ((S, S¢),(T, T¢)) ~ (S, S¢),
то есть пары сил (Р, Р ¢) и (S, S¢) эквивалентны.
Остается доказать эквивалентность пар (S, S¢) и (F, F ¢). Поскольку эти пары имеют равные плечи, они будут эквивалентны, если будут равны их моменты.
По условию теоремы моменты пар (Р, Р ¢) и (F, F ¢) равны. Таким образом:
M (F, F ¢) = M (Р, Р ¢) = M (Р 1, Р 1 ¢) = MC (Р 1).
В силу теоремы Вариньона:
MC (Р 1) = MC (S) + MC (T) = MC (S),
поскольку линия действия силы T проходит через точку С и ее момент равен нулю. Итак:
M (F, F ¢) = MC (S) = M (S, S¢),
а значит пары (S, S¢) и (F, F ¢) будут эквивалентны.
Таким образом: (Р, Р ¢) ~ (S, S¢) ~ (F, F ¢), и теорема доказана.
Рассмотрим следствия этой теоремы, которые также можно рассматривать как свойства пар сил в дополнение к свойствам, рассмотренным в § 3.2.
Следствия:
1. Действие пары сил на ТТ не меняется при ее перемещении в своей плоскости.
2. Действие пары сил на ТТ не изменится, если одновременно изменить плечо и силы пары, сохранив неизменным ее момент.
Рассмотрим в частности пару, представленную силами ± P = M /2e, приложенными к балке в точках х=хМ ±e (Рис.3.5а). Плечо такой пары, равно 2e, а ее момент равен M. При изменении e будут меняться плечо и силы пары, но величина ее момента останется равной первоначальному значению.
Определение 3.3. Моментом называется система, полученная из пары сил ± P = M /2e, при e®0.
Таким образом, термин «момент» имеет в ТМ два значения: 1) момент как произведение силы на ее плечо и 2) момент как система, полученная из пары сил в соответствии с определением 3.3.
Отметим, что при таком предельном переходе плечо пары стремится к нулю, а силы пары – к бесконечности. Полученный в соответствии с определением 3.3 момент фактически является таким же самостоятельным объектом в механике, как и сила, и в дальнейшем мы будем обозначать его так, как показано на рис.3.5б.
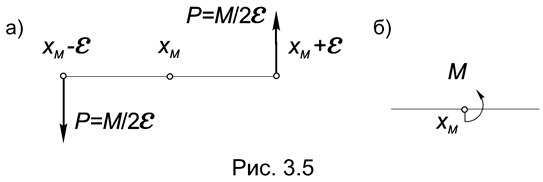
Если для абсолютно твердого тела последний момент эквивалентен паре сил, показанной на рис. 3.5а, то в механике деформируемого тела действие такого сосредоточенного момента, приложенного в точке х = хМ , существенно отличается от действия пары сил.
Теорема 3.3. (Об эквивалентности пар в пространстве). Две пары, лежащие в параллельных плоскостях и имеющие равные по величине и по знаку моменты, эквивалентны.
Для доказательства этой теоремы нам понадобится следующая
Лемма. Равнодействующая двух параллельных и равных по модулю сил равна их сумме, а ее линия действия проходит посредине между точками их приложения (Рис.3.6).
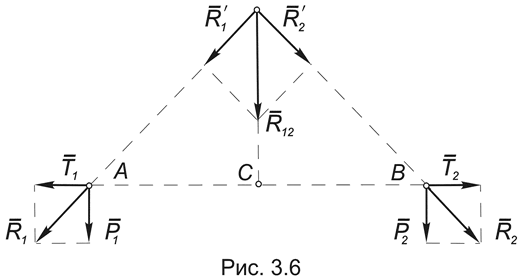
Для доказательства леммы достаточно к системе двух сил (P 1, P 2), приложенных соответственно в точках A и B, о которых идет речь в теореме, добавить уравновешенную систему сил (T 1, T 2), а затем воспользоваться аксиомой параллелограмма:
(P 1, P 2) ~ ((P 1, P 2), (T 1, T 2)) ~ ((P 1, T 1), (P 2, T 2)) ~ (R 1, R 2) ~ (R 12 ),
где P 1 = P 2 = P, R 12 = 2 P, а AС = BC.
Переходя к доказательству теоремы, рассмотрим две пары сил (P 1, P 2) и (F 1, F 2), имеющие равные моменты и лежащие в параллельных плоскостях П1 и П2 соответственно (Рис.3.7).
Построим в плоскости П2 отрезок CD, равный и параллельный отрезку АВ и приложим в точках C и D две системы уравновешенных сил: (S 1, S 2) ~ 0 и (T 1, T 2) ~ 0, выбрав силы S и T равными по модулю и параллельными силам P.
На основании аксиом 2, 3 и последней леммы:
(P 1, P 2) ~ ((P 1, P 2), (S 1, S 2), (T 1, T 2)) ~ ((P 1, T 1), (P 2, S 2), (S 1, T 2)) ~
~ ((R 1, R 2), (S 1, T 2)) ~ (S 1, T 2),
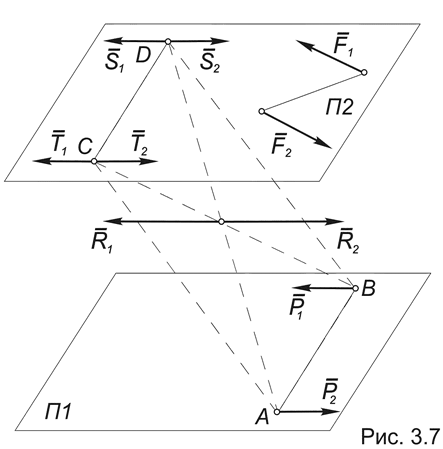
поскольку R 1 ~ (P 1, T 1) и R 2 ~ (P 2, S 2) также образуют уравновешенную систему сил, которую можно исключить.
Таким образом, мы получили две пары сил: (S 1, T 2) и (F 1, F 2), которые лежат в одной плоскости и имеют равные по величине и по знаку моменты. В силу предыдущей теоремы 3.2 они будут эквивалентны, откуда следует, что
(P 1, P 2) ~ (S 1, T 2) ~ (F 1, F 2).
Теорема доказана.
Следствие. Действие пары сил на ТТ не изменится при ее перемещении в параллельную плоскость, расположенную в пределах этого тела.
ПРИМЕЧАНИЕ. В силу этого следствия вектор-момент пары сил в пределах этого тела можно считать свободным.
Сложение пар сил
Теорема 3.4. Две пары, лежащие в пересекающихся плоскостях, эквивалентны одной паре с вектор-моментом, равным геометрической сумме вектор-моментов слагаемых пар.
Для доказательства рассмотрим две пары сил (P 1, P 2) и (F 1, F 2), лежащие в плоскостях П1 и П2 соответственно, которые пересекаются по прямой АВ.
Не уменьшая общности можно считать, что плечи этих пар равны отрезку АВ этой прямой. Пусть М (P 1, P 2) = М 1, а М (F 1, F 2) = М 2 (Рис.3.8).
Воспользовавшись аксиомой параллелограмма, получим:
((P 1, P 2), (F 1, F 2)) ~ ((P 1, F 1), (P 2, F 2)) ~ (R 1, R 2).
При этом момент результирующей пары с учетом теоремы Вариньона будет равен:
М (R 1, R 2) = М А (R 1) = М А (P 1) + М А (F 1) = М (P 1, P 2) + М (F 1, F 2) = М 1 + М 2.
Теорема доказана.
Следствия:
1. Система n пар в пространстве эквивалентна одной паре с вектор-моментом, равным геометрической сумме вектор-моментов слагаемых пар:
М =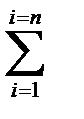 
М i (3.3)
2. Система n пар на плоскости эквивалентна одной паре с моментом, равным алгебраической сумме моментов слагаемых пар:
М = 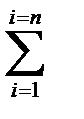Мi (3.4)
ПРИМЕЧАНИЕ. В соответствии с замечанием в конце предыдущего параграфа вектор-момент пары сил в пределах рассматриваемого тела, как в математике, является свободным, поэтому последняя теорема может показаться излишней.
В действительности между векторами в математике и векторами в ТМ продолжает оставаться различие, которое обнаруживается при рассмотрении системы аксиом, которым удовлетворяют векторы в математике и не удовлетворяют вектора сил.
Равновесие систем пар
Система пар сил, приложенных к ТТ, будет уравновешена, если момент результирующей пары равен нулю.
Таким образом, из соотношений (3.3) и (3.4) следуют условия равновесия системы пар:
1. Необходимым и достаточным условием равновесия системы пар в пространстве является равенство нулю геометрической суммы вектор-моментов слагаемых пар:
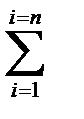М i = 0. (3.5)
2. Необходимым и достаточным условием равновесия системы пар на плоскости является равенство нулю алгебраической суммы моментов слагаемых пар:
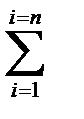Мi = 0. (3.6)
Условие (3.5) имеет геометрическую интерпретацию и означает замкнутость многоугольника, образованного из векторов моментов пар.
Пример 3.1. Определить опорные реакции рамы, загруженной системой пар (Рис.3.9).
Решение. Заменим систему пар, приложенных к раме, результирующей парой по формуле (3.4): MR = M 1 - M 2 + M 3 = 3 - 4 + 7 = 6 кНм.
Из условия равновесия систем пар (3.6) следует, что активную пару MR, приложенную к раме, может уравновесить только пара сил, образованных опорными реакциями, поэтому линия действия RA должна быть параллельной RВ и
MR + M (RA, RВ) = 0,
откуда RA = RВ = MR / d, где d = 6cos30°= 3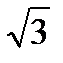 
м - плечо пары (RA, RВ).
Итак, RA = RВ = 6/(3 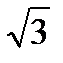) = (2 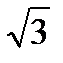)/3 м. ·
