Приведение двух параллельных сил

В ходе рассмотрения такой системы сил возможны три следующих случая приведения.

1. Система двух коллинеарных сил. Рассмотрим систему двух параллельных и направленных в одну сторону сил P и Q, приложенных в точках А и В. Будем считать, что силы перпендикулярны к этому отрезку (Рис.7.1а).

Выберем в качестве центра приведения точку С, принадлежащую отрезку АВ и удовлетворяющую условию:

АС / СВ = Q / P. (7.1)

Главный вектор системы R_C = P + Q по модулю равен сумме этих сил: R_C = P + Q.

Главный момент относительно центра С с учетом (7.1) равен нулю: M _C = = P × АС - Q × СВ = 0.

Таким образом, в результате приведения мы получили: R_C ¹ 0, M _C = 0. Это означает, что главный вектор эквивалентен равнодействующей, проходящей через центр приведения, то есть:

Равнодействующая коллинеарных сил равна по модулю их сумме, а ее линия действия делит отрезок, соединяющий точки их приложения, обратно пропорционально модулям этих сил внутренним образом.

Отметим, что положение точки С не изменится, если силы Р и Q повернуть на угол a. Точка С, обладающая таким свойством называется центром параллельных сил.

2. Система двух антиколлинеарных и не равных по модулю сил. Пусть силы P и Q, приложенные в точках А и В, параллельны, направлены в противоположные стороны и по модулю не равны (Рис.7.1б).

Выберем в качестве центра приведения точку С, удовлетворяющую по-прежнему соотношению (7.1) и лежащую на той же прямой, но за пределами отрезка АВ.

Главный вектор этой системы R_C = P + Q по модулю теперь будет равен разности модулей векторов: R_C = Q - P.

Главный момент относительно центра С по-прежнему равен нулю: M _C = = P × АС - Q × СВ = 0, поэтому

Равнодействующая антиколлинеарных и не равных по модулю сил равна их разности, направлена в сторону большей силы, а ее линия действия делит отрезок, соединяющий точки их приложения, обратно пропорционально модулям этих сил внешним образом.

3. Система двух антиколлинеарных и равных по модулю сил. Возьмем за исходный предыдущий случай приведения. Зафиксируем силу Р, а силу Q устремим по модулю к силе Р.

Тогда при Q ® Р в формуле (7.1) отношение АС / СВ ® 1. Это означает, что АС ® СВ, то есть расстояние АС ® .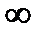

При этом модуль главного вектора R_C ® 0, а модуль главного момента не зависит от положения центра приведения и остается равным первоначальному значению:

M_C = P × АС - Q × СВ = P (АС - СВ) = P × АB.

Итак, в пределе мы получили систему сил, для которой R_C = 0, M_C ¹ 0, а центр приведения удален в бесконечность, которую нельзя заменить равнодействующей. В этой системе нетрудно узнать пару сил, поэтому

Пара сил равнодействующей не имеет.