Во многих случаях решение задач можно упростить, если вместо уравнений равновесия или в дополнение к ним непосредственно использовать условия равновесия, аксиомы и теоремы статики. Соответствующий подход и получил название графического определения опорных реакций.
Прежде чем перейти к рассмотрению графического метода отметим, что, как и для системы сходящихся сил, графически можно решить только те задачи, которые допускают аналитическое решение. При этом графический метод определения опорных реакций удобен при небольшом числе нагрузок.
Итак, графический метод определения опорных реакций основан главным образом на использовании:
- аксиомы 2 (о равновесии системы двух сил);
- аксиомы 5 (о действии и противодействии);
- теоремы о трех силах;
- условия равновесия плоской системы сил.
При графическом определении реакций составных систем рекомендуется следующая последовательность рассмотрения:
- выбрать тело с минимальным числом алгебраических неизвестных реакций связей;
- если таких тел два или больше, то начать решение с рассмотрения тела, к которому приложено меньшее число сил;
- если таких тел два или больше, то выбрать тело, для которого большее число сил известно по направлению.
Пример 5.7. Определить графически опорные реакции рамы, изображенной на рис.5.9.
Решение. Система состоит из двух тел, имеющих равное число алгебраических неизвестных: 4 - для АС (XA, YA, XC, YC) и 4 - для ВС (XB, YB, XC ¢, YC ¢), но на тело АС действуют три силы (P, RA, RC), а на ВС - только две (RВ, RC ¢), поэтому начинаем решение с рассмотрения тела ВС.
Согласно второй аксиоме RВ и RC ¢действуют вдоль прямой, соединяющей точки их приложения, то есть по прямой ВС.
Рассмотрим равновесие всей рамы АВС как твердого тела. На нее действует уравновешенная система трех непараллельных сил, которая в силу теоремы о трех силах должна быть сходящейся, поэтому реакция RA должна проходить через точку К, где пересекаются линии действия RВ и RC ¢ (Рис.5.13а).
Строим силовой треугольник, проводя через начало и конец вектора Р прямые, параллельные направлениям RA и RВ до их пересечения (Рис.5.13б).
Из подобия силового треугольника Oab и треугольника ВАК на чертеже находим искомые реакции:
RВ / P = (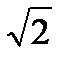
)/4; ð RВ = (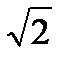)/4; XВ = - (RВ 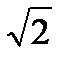)/2 = - P /4; YВ = P /4.
½ XА ½/ P = 3/4; XА = - (3/4) P; YА = - P /4. ·
Пример 5.8. Определить графически опорные реакции рамы, показанной на рис. 5.11.
Решение. Как и в предыдущем примере, начинаем рассмотрение с части, на которую действуют только две силы, и по аксиоме 2 определяем линию действия RA (Рис.5.14).
Рассматривая равновесие рамы в целом, приходим к заключению, что опорные реакции RA и RВ должны составить пару, которая уравновесит приложенный к раме момент. Отсюда следует, что RA = RВ = М / 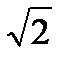, при этом
XА = YА = RA (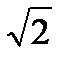 /2) = М /2; XВ = YВ = - М /2. ·
