Рассмотрим тело, которое закреплено в центре О и может поворачиваться вокруг оси, проходящей через точку О и перпендикулярной к плоскости чертежа. Приложим в точке А этого тела силу P и выясним, чем определяется вращательное действие этой силы (Рис.3.1).

Очевидно, что воздействие силы на тело будет зависеть не только от ее величины, но и от того, как она направлена, и в конечном итоге будет определяться ее моментом относительно центра О.
Определение 3.1. Моментом силы Р относительно центра О называется взятое со знаком  произведение модуля силы на ее плечо - то есть длину перпендикуляра, опущенного из моментной точки на линию действия силы.
произведение модуля силы на ее плечо - то есть длину перпендикуляра, опущенного из моментной точки на линию действия силы.
Правило знаков: момент силы считается положительным, если сила стремится повернуть тело против хода часовой стрелки и отрицательным, если она вращает тело по ходу часовой стрелки.
В соответствии с данным определением момент силы численно равен удвоенной площади треугольника OAB, построенного на векторе силы P с вершиной в моментной точке: M 0(P) = P × d = 2 S D OAB.
Отметим, что момент силы относительно точки О равен нулю, если линия действия силы проходит через моментную точку.
Рассмотренное определение момента силы подходит только для плоской системы сил. В общем случае для однозначного описания вращательного действия силы введем следующее определение.
Определение 3.2. Вектор-моментом силы Р относительно центра О называется вектор, который:
- приложен в моментной точке О перпендикулярно к плоскости треугольника, построенного на векторе силы с вершиной в моментной точке;
- направлен по правилу право винта;
- равен по модулю моменту силы Р относительно центра О (Рис3.2а).
Правило правого винта, известное также из курса физики как правило буравчика, означает, что если смотреть навстречу вектор-моменту М 0(Р), мы увидим вращение силой Р плоскости своего действия, происходящим против хода часовой стрелки.
Обозначим через r радиус-вектор точки приложения силы Р и докажем, что справедлива следующая
Теорема 3.1. Вектор-момент силы Р относительно центра О равен векторному произведению радиус-вектора r и вектора силы Р:
М 0(Р) = (r  Р). (3.1)
Р). (3.1)
Напомним, что векторным произведением векторов a и b и называется вектор c, который (Рис.3.2б):

- перпендикулярен к векторам a и b;
- образует с ними правую тройку векторов, то есть, направлен так, что,
смотря навстречу этому вектору, мы увидим поворот от вектора a к вектору b на наименьший угол происходящим против хода часовой стрелки;
- равен по модулю удвоенной площади треугольника, построенного на этих векторах:
½ c ½ = ½ a 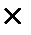 b ½ = ½ a ½×½ b ½×sin (a, b).
b ½ = ½ a ½×½ b ½×sin (a, b).
Для доказательства теоремы отметим, во-первых, что вектор, равный векторному произведению векторов r и Р будетколлинеарным вектору М 0(Р). Чтобы убедиться в этом, достаточно отложить эти векторы от одной точки (Рис.3.2в). Итак, (r 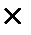 Р) М 0(Р).
Р) М 0(Р).
Во-вторых, модуль векторного произведения этих векторов будет равен:
½ r 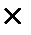 Р ½= ½ r ½×½ Р ½× sin (r, Р) = P × d =½ М 0(Р)½,
Р ½= ½ r ½×½ Р ½× sin (r, Р) = P × d =½ М 0(Р)½,
откуда и следует соотношение (3.1).Следствием теоремы (3.1) является
Теорема Вариньона (о моменте равнодействующей сходящихся сил). Вектор-момент равнодействующей системы сходящихся сил относительно произвольного центра О равен геометрической сумме вектор-моментов всех сил системы относительно этого центра:
М 0(R) = 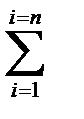 М 0 i (Pi). (3.2)
М 0 i (Pi). (3.2)
В самом деле, момент равнодействующей с учетом (3.1) и (2.3) будет равен:
М 0(R) 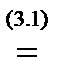 r
r  R
R 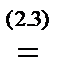 r
r 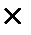
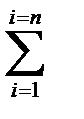 Pi =
Pi = 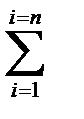 (ri
(ri 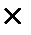 Pi) =
Pi) = 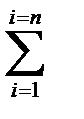 М 0 i (Pi).
М 0 i (Pi).
Для плоской системы сходящихся сил геометрическая сумма в (3.2) переходит в алгебраическую:
М 0(R) = 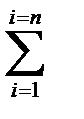 М 0 i (P i).
М 0 i (P i).
ПРИМЕЧАНИЕ. В учебной литературе термин «момент» применяют для обозначения как момента силы, так и ее вектор-момента.
Пара сил и ее свойства
Определение. Парой называется система двух сил, которые равны по модулю, параллельны и направлены в противоположные стороны.
Пара, приложенная к ТТ, стремится вызвать его вращение. Вращательное действие пары определяется ее моментом, который равен произведению одной из сил пары на ее плечо, то есть расстояние между линиями действия сил пары:
M (P, P ¢) = P × d = P ¢× d.
Нетрудно убедиться в справедливости следующих утверждений:
1) Сумма проекций сил пары на любую ось равна нулю;
2) Сумма моментов сил пары относительно любой точки равна моменту этой пары.
В общем случае действие пары сил на ТТ определяется тремя факторами:
- плоскостью действия;
- направлением вращения в этой плоскости;
- величиной момента.
Чтобы однозначно определить все эти факторы, вводят понятие вектор-момента пары.
Определение. Вектор-моментом пары сил называется вектор, который:
- перпендикулярен плоскости действия пары;
- направлен по правилу правого винта;
- равен по модулю моменту пары (Рис.3.3).
Нетрудно убедиться, что вектор-момент пары сил можно представить в виде векторных произведений:
М (Р, Р ¢) = АВ 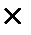 Р ¢ = ВА
Р ¢ = ВА 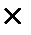 Р.
Р.

ПРИМЕЧАНИЕ. В последнем определении ничего не сказано о точке приложения вектор-момента пары сил. Обоснования этого будут даны в следующем параграфе.






