Пусть система сходящихся сил задана аналитически, то есть, известны координаты центра системы A (x, y, z) и проекции каждой силы на оси координат: Xi, Yi, Zi, где индекс i принимает значения от 1 до n.
Согласно теореме 2.2 равнодействующая системы приложена в точке A и равна геометрической сумме этих сил:
(P 1, P 2,..., P n) ~ R = 
P i. (2.3)
Представим каждую силу системы в виде суммы ее составляющих по осям координат - как в формуле (2.1):
Р i = Xi× i + Yi × j + Zi× k. (2.4)
В аналогичной форме запишем неизвестную пока равнодействующую R:
R = Rx i + Ry j + Rz k. (2.5)
Подставляя (2.5) и (2.4) в (2.3) и приравнивая коэффициенты при одинаковых ортах в обеих частях последнего соотношения, получим искомые выражения проекций равнодействующей:
Rx = S Xi; Ry = S Yi ; Rz = S Zi. (2.6)
Полученные зависимости можно сформулировать в виде следующей теоремы: проекция равнодействующей системы на какую-либо ось равна сумме проекций всех сил системы на эту ось.
Воспользовавшись формулами (2.2), найдем модуль и направление равнодействующей произвольной пространственной системы сходящихся сил:
 =  ;
cos (R, i) = Rx / R; cos (R, j) = Ry / R; cos (R, k) = Rz / R..
|
(2.7)
Условия и уравнения равновесия системы сходящихся сил
Для того чтобы система сходящихся сил была уравновешенной, ее равнодействующая должна равняться нулю. В силу теоремы 2.2 отсюда следует условие равновесия системы сходящихся сил:
R = S P i = 0. (2.8)
Условие (2.8) можно интерпретировать графически или аналитически. Графически это означает, что при построении силового многоугольника конец последнего вектора совпадет с началом первого. Это называется замкнутостью силового многоугольника.
Аналитически из условия (2.8) с учетом формул (2.7) получаются уравнения равновесия произвольной пространственной системы сходящихся сил:
S Xi = 0;S Yi = 0;S Zi = 0. (2.9)
Для плоской системы сходящихся сил, лежащих в плоскости Oxy, соответствующие уравнения равновесия примут вид:
S Xi = 0;S Yi = 0. (2.10)
Решение задач
При решении задач по статике рекомендуется придерживаться следующего плана:
1) выбрать тело, равновесие которого будем рассматривать;
2) приложить к нему активные силы;
3) отбросить связи, заменив их неизвестными опорными реакциями;
4) определить эти реакции аналитически, используя уравнения равновесия (2.9) и (2.10) или графически, используя условие замкнутости силового многоугольника;
5) проверить правильность решения задачи.
Пример 2.1. Определить реакции стержней, соединенных шарниром В, если к нему подвешен груз весом Q (Рис.2.4а).
Решение. В соответствии с предложенным выше планом выбираем тело, равновесие которого мы будем рассматривать. Этот выбор, в основном, определяется условиями задачи. Если в этой задаче рассмотреть равновесие подвешенного груза, то мы сумеем найти только силу натяжения нити, которая равна весу тела: T = Q (Рис.2.4б).
Чтобы определить реакции стержней, рассмотрим равновесие точки В. Можно считать, что к ней посредством нити приложена активная сила Q и реакции отброшенных стержней SA и SC (Рис.2.3в).
Решим эту задачу аналитически. Выбирая начало отсчета в точке В, составим уравнения (2.10), которые в этой задаче примут вид:
- SA cosa + SC cosb = 0;
SA sina + SC sinb = Q.
Чтобы найти отсюда SC сложим полученные уравнения, умножив предварительно первое из них на sina, а второе – на cosa:
SC (sinacosb + cosa sinb) = Q cosa.
Отсюда следует, что SC = Q cosa/sin(a+b), а поскольку a и b в эти уравнения входят симметрично, то SA = Q cosb/sin(a+b).
Для проверки правильности аналитического решения задачи воспользуемся графическим методом.
Треугольник, образованный из трех сил: Q, SA и SC должен быть замкнут, поэтому решение сводится к построению треугольника по известной стороне (Q) и направлению двух других сторон(SA и SC). Для этого нужно в масштабе построить вектор Q, а затем из начала и из конца этого вектора провести прямые, параллельные SA и SC до их пересечения (Рис.2.4г).
Измерив длины найденных отрезков и пересчитав в масштабе, можно считать поставленную задачу решенной. Направление полученных векторов определяется из условия замкнутости силового многоугольника, то есть конец последнего вектора должен совпадать с началом первого.
Можно, впрочем, определить величину SA и SC и без масштабной линейки, если просто решить построенный треугольник.
С этой целью воспользуемся теоремой синусов:
,
откуда, заменяя синус дополнительного угла косинусом, получим:
SA = Q cosb/sin(a+b); SC = Q cosa/sin(a+b).
То есть, результат графического решения совпадает с аналитическим, значит задача решена правильно. ·
Пример 2.2. Центр невесомого идеального блока удерживается при помощи двух стержней, соединенных шарнирно в точке В. Через блок переброшена нить, один конец которой закреплен, а к другому – подвешен груз весом Q (Рис.2.5а). Определить реакции стержней, пренебрегая размерами блока.
Решение. Рассмотрим равновесие блока В, к которому приложены силы натяжения нитей Т 1 и Т 2 и реакции отброшенных стержней SA и SС, которые, как и в предыдущем примере мы считаем растянутыми (Рис.2.5б).
Фактически в качестве активной силы выступает вес груза Q, который приложен к блоку с помощью нити, поэтому Т 1 = Q. По поводу силы Т 2 надо отметить, что идеальным – то есть без трения блоком называется механизм, который меняет направление силы натяжения нити, но не ее величину, поэтому Т 1 = Т 2 = Q.
Пренебрегая размерами блока, получим уравновешенную систему сходящихся сил, приложенных в точке В (Рис.2.5в).
Определим реакции SA и SС аналитически. Отметим, что если в первое из уравнений (2.10) входят оба неизвестных, то в уравнение S Yi = 0 неизвестная реакция SС не войдет, поэтому имеет смысл начать решение задачи именно с этого уравнения:
SA cos30°+ Т 2 cos60°- Т 1 = 0.
Подставляя сюда значения тригонометрических функций и Т 1 = Т 2 = Q, получим:
SA 
= 
,
откуда SA = Q (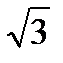
/3).
Теперь вернемся к уравнению S Xi = 0:
- SA cos60°+ Т 2 cos30°+ SС = 0,
или
SС = SA /2 - Q (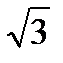 /2).
Подставив найденное выше значение SA, получим:
SС = Q (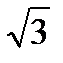 /6) - Q ( 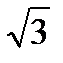/2) = - Q ( 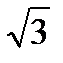/3).
При этом минус в последнем выражении означает, что стержень ВС не растянут, как мы предполагали, а сжат.
Для проверки полученного результата решим эту задачу графически. С этой целью от центра О последовательно откладываем в масштабе известные силы Т 1 и Т 2, затем от начала первого и от конца последнего вектора проводим прямые, параллельные SA и SС до их пересечения (Рис.2.5г).
Нетрудно видеть, что построенный силовой многоугольник имеет ось симметрии и ½ SA ½ = ½ SС ½. При этом направление вектора SС на силовом многоугольнике противоположно первоначальному направлению, указанному на чертеже, то есть стержень ВС не растянут, а сжат. ·
ПРИМЕЧАНИЯ:
1. В системе уравнений (2.10) оси координат не обязательно должны быть взаимно перпендикулярными, поэтому, если в последнем примере выбрать ось Ох, совпадающую по направлению с силой Т 2 , мы получим систему уравнений, из которых неизвестные SA и SС находятся независимо одно от другого.
2. Впоследствии мы увидим, что аналитическое решение можно проверить не только с помощью графического решения, но и аналитически. Впрочем, для системы сходящихся сил изложенный метод решения задач является, по-видимому, оптимальным.
ГЛАВА 3. ТЕОРИЯ ПАР СИЛ
