Если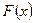 
одна из первообразных для непрерывной на 
функции 
, то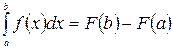 
(Формула Ньтона – Лейбница).
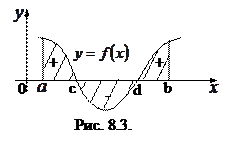
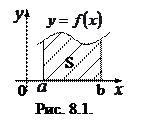
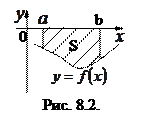Известно, что если 
и непрерывна на , то площадь криволинейной трапеции, изображенной на рисунке 8.1., равна 
(8.1).
Если на отрезке 
и непрерывна (рис. 8.2), то определенный интеграл (8.1) будет неположительным. По абсолютной величине он будет
 | |||
 | |||
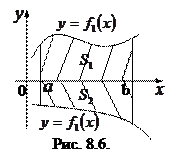
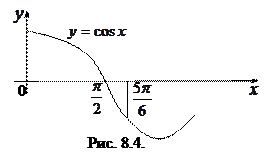
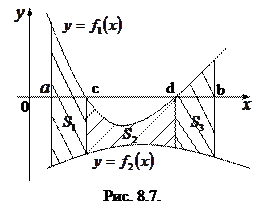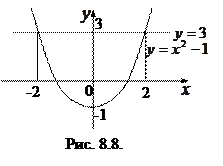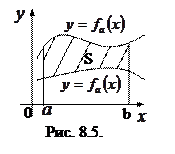
равен плоди криволинейной трапеции, изображенной на рис. 8.2. Тогда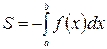 
. Объединяя полученные результаты, запишем формулу вычисления площадей фигур для случаев, изображенных на рис. 8.1 и 8.2. 
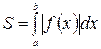. Если непрерывная функция 
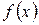меняет знак на конечное число раз (рис. 8.3.), то для вычисления площади заштрихованной фигуры необходимо отрезок разбить на отрезки, соответствующие знакопостоянству . Тогда
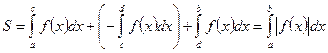. (8.3)
Пример 8.1. Вычислить площадь фигуры, ограниченной косинусоидой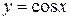 
и осью 
на промежутке 
.
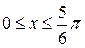Решение. Так как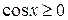 
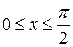при 
и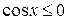 
, 
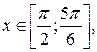то получаем (рис.8.4)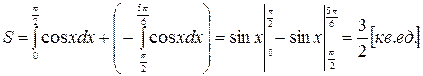 
Рассмотрим задачи, связанные с вычислением площадей фигур, ограниченных двумя кривыми 
, 
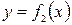и прямыми 
, 
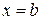(рис.8.5, 8.6, 8.7). Если на отрезке выполнено условие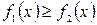 
, то для всех трех случаев получаем 
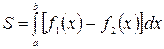(8.4).
Для случая, изображенного на рис. 8.5 равенство очевидно.
Для рис. 8.6. получаем
.
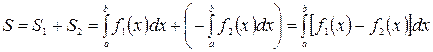Для фигуры, изображенной на рис. 8.7, имеем
.
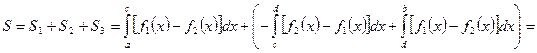
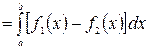Равенство (8.4) справедливо и при любом другом расположении кривых. Необходимым условием при этом является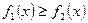 
.
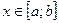Пример 8.2. Найти площадь фигуры, ограниченной линиям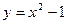и 
и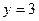 
.
Решение: Находим точки пересечения параболы с прямой:
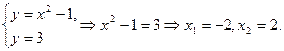
Тогда (рис.8.8)
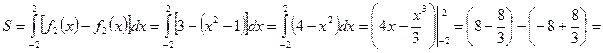
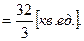
Пусть кривая задана параметрически
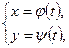
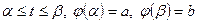(8.5)
причем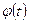 
и 
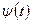непрерывно дифференцируемые функции.
Уравнения (8.5) задают неявно некоторую функцию 
на отрезке . Тогда площадь соответствующей криволинейной трапеции
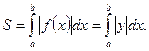
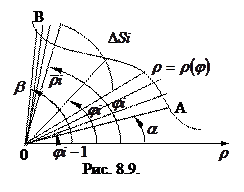Используя замену переменной, получаем: 
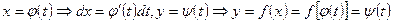и 
Пример 8.3. Вычислить площадь круга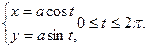 
Решение.
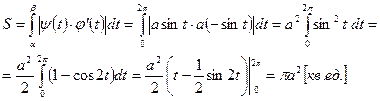
Пусть линия задана в полярной системе координат: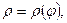 
где 
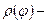непрерывная функция при 
.
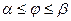Площадь криволинейного сектора ОАВ на рисунке 8.9 определяется выражением:
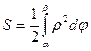(8.8)
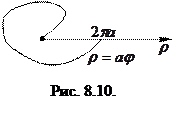Пример 8.4. Вычислить площадь, ограниченную одним витком спирали Архимеда 
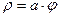и полярной осью 
(рис.8.10).
Решение: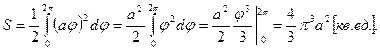 
Длина дуги плоской кривой.
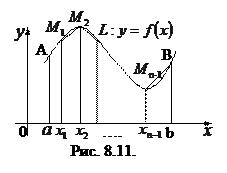
Длиной дуги 
называется предел длины вписанной ломанной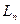 
(рис. 8.11) при 
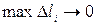, если этот предел существует и не зависит от способа разбиения дуги на части.
Для случая, когда и 
непрерывные на функции (если и непрерывны на , то кривую называют гладкой).
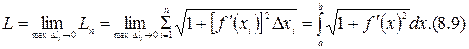
Пример 8.5. Найти длину дуги кривой 
от точки 
до точки с координатами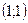 
.
Решение: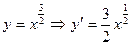 
. 
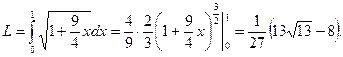
Если кривая задана параметрически в виде
, 
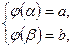где 
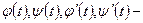непрерывные на 
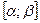функции, то, используя замену переменной
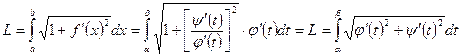(8.10)
Для кривой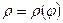 
, заданной в полярной системе (если )
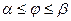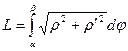(8.11)
Вычисление объема тела.
Рассмотрим тело, ограниченное замкнутой поверхностью (рис. 8.12) и решим задачу о вычислении его объема. Для этого выберем какую – либо направленную прямую в качестве оси 
, задав на ней точку начала 0. Плоскостью, перпендикулярной оси рассечем тело. Тогда в сечении получим плоскую фигуру, площадь которой будет зависеть от положения секущей плоскости на оси :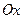 
.
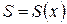Объем тела, заключенного между плоскостями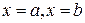 
.
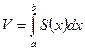(8.12)
Формула (8.12) позволяет находить объем тел по площадям параллельных сечений.
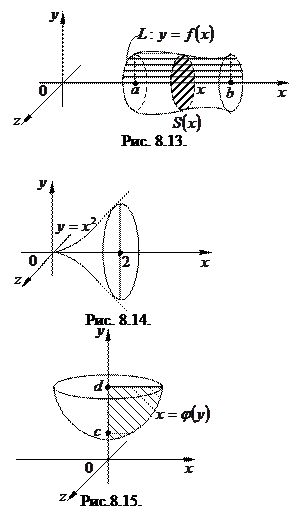Пусть непрерывная на функции, задающая кривую (рис. 8.13). Пусть вращением криволинейной трапеции вокруг оси 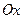получено тело вращения. Найдем объем такого тела.
Заметим, что в любом из сечений тела плоскостями, перпендикулярными оси 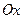, получаем круг с радиусом 
. Тогда площадь сечения в точке 
будет равна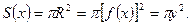 
причем в силу непрерывности функция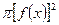 
также непрерывна. Тогда по формуле (8.12) находим объем тела 
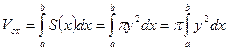(8.13).
Пример 8.6. Парабола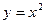 
вращается вокруг оси 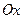(8.14). Найти объем тела вращения, заключенного между 
, 
.
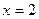Решение: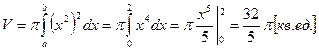 
.
Если тело получено вращением криволинейной трапеции вокруг оси 
, то по аналогии с формулой (8.13) получаем (рис 8.15)
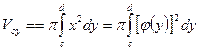(8.14)
