Числовая последовательность – функция, определенная на множестве  натуральных чисел
натуральных чисел  . Если множество значений ограничено – последовательность ограниченная. Такая последовательность может иметь предел. Пределом называют число, если существует точное
. Если множество значений ограничено – последовательность ограниченная. Такая последовательность может иметь предел. Пределом называют число, если существует точное  (номер члена последовательности) начиная с которого восполняется неравенство
(номер члена последовательности) начиная с которого восполняется неравенство  , где
, где  - сколько угодно малое положительное число. Обозначение:
- сколько угодно малое положительное число. Обозначение: 
Пример 1.5. Вычислить предел последовательности


Решение задач упрощается, если школьный курс усвоен и есть навык алгебраических преобразований. Легко видеть, что в числителе дроби – арифметическая прогрессия  ;
;  . Сумма членов
. Сумма членов  , подставив в исходное выражение получим
, подставив в исходное выражение получим  (поскольку предел суммы равен сумме пределов)=
(поскольку предел суммы равен сумме пределов)= 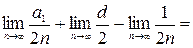
 =
= 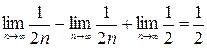
(первые два слагаемых компенсируют друг друга, а предел постоянной равен самой постоянной)
1.3 Предел функции. Бесконечно малые и бесконечно большие величины (функции). Замечательные пределы.
Говорят, что предел функции  при
при  (стремящемся к
(стремящемся к  ) равен
) равен 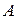 , если для любого
, если для любого  найдется
найдется  такое, что
такое, что  если
если  .
.  . Предел может существовать и при
. Предел может существовать и при  , что записывают так:
, что записывают так:  . Если при
. Если при  функция неограниченно возрастает пишут
функция неограниченно возрастает пишут 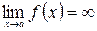 и функцию называют бесконечно большой при
и функцию называют бесконечно большой при  . Если
. Если  функцию называют бесконечно малой при
функцию называют бесконечно малой при  .
.
Из теорем о пределах напомним следующие:
1.  , где
, где  .
.
2. 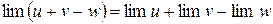 .
.
3.  .
.
4.  .
.
 функции, имеющие предел.
функции, имеющие предел.
Пример 1.6. а) найти предел 
Непосредственная подстановка приводит к неопределенности вида  (этот символ означает, что при
(этот символ означает, что при  неограниченно возрастают
неограниченно возрастают  и числитель и знаменатель). Разделим почленно на
и числитель и знаменатель). Разделим почленно на  числитель и знаменатель дроби и найдем предел:
числитель и знаменатель дроби и найдем предел: 
Здесь и во всех других случаях пределы дробей с постоянным (или ограниченным числителем) и бесконечно возрастающим знаменателем равны нулю: 
Если показатель старшей степени многочлена в числителе выше, чем в знаменателе, то тот же прием приводит в пределе к выражению вида  , где
, где  постоянная.
постоянная.
б) Найти предел  .
.
Решение. Разделив почленно на  , получим
, получим  .
.
Если показатель старшей степени многочлена в числителе ниже, чем в знаменателе, то такой прием приводит в пределе к выражению вида 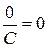 .
.
в) Найти предел 
Решение. Разделив почденно числитель и знаменатель на  , получим:
, получим:
 .
.
Пусть требуется найти предел функции  при
при  , где числитель и знаменатель – многочлены, которые при
, где числитель и знаменатель – многочлены, которые при  оба равны нулю. Приходим к неопределенности
оба равны нулю. Приходим к неопределенности  , которую можно раскрыть, воспользовавшись теоремой Безу: если многочлен при
, которую можно раскрыть, воспользовавшись теоремой Безу: если многочлен при  обращается в нуль, он делится на двучлен
обращается в нуль, он делится на двучлен  . Следовательно, числитель и знаменатель дроби можно разложить на множители:
. Следовательно, числитель и знаменатель дроби можно разложить на множители:


После сокращения дроби на  придем к пределу
придем к пределу  .
.
Если при  и этот предел приведет к неопределенности
и этот предел приведет к неопределенности  , разложение на множители повторяют. В итоге неопределенность раскрывается.
, разложение на множители повторяют. В итоге неопределенность раскрывается.
Пример 1.7. а) Найти предел  .
.
Решение. Так как при  числитель
числитель  и знаменатель
и знаменатель  , то оба эти квадратные трехчлена можно разложить на множители, один из которых будет
, то оба эти квадратные трехчлена можно разложить на множители, один из которых будет  . Разложение можно выполнить путем деления многочленов на двучлен
. Разложение можно выполнить путем деления многочленов на двучлен  :
:

б) Найти предел 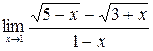 .
.
Решение. Подставляя  , придем к неопределенности вида
, придем к неопределенности вида  . Умножим числитель и знаменатель дроби на сумму
. Умножим числитель и знаменатель дроби на сумму  с таким расчетом, чтобы избавиться от иррациональности в числителе и устранить неопределенность. Поскольку
с таким расчетом, чтобы избавиться от иррациональности в числителе и устранить неопределенность. Поскольку
 , то
, то
 .
.
Существенно упрощает решение задач использование двух важных соотношений теории пределов, называемых первым  и вторым
и вторым  замечательными пределами и следствий из них, аналитически записанных так:
замечательными пределами и следствий из них, аналитически записанных так:  (1.1);
(1.1);  (1.2);
(1.2);  (1.3);
(1.3);  (1.4).
(1.4).
Отметим, что второй замечательный предел раскрывает неопределенность вида  (основание степени
(основание степени 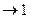 , а показатель
, а показатель  ) и равен числу е, основанию натурального логарифма
) и равен числу е, основанию натурального логарифма  . Помимо перечисленных, встречаются неопределённости вида:
. Помимо перечисленных, встречаются неопределённости вида: 
Задача состоит в раскрытии неопределённостей при помощи тождественных преобразовании функции или подстановок.
Пример 1.8. а) 
Здесь тоже получаем неопределённость  . Выполним тригонометрические преобразования, которые позволят воспользоваться первым замечательным пределом.
. Выполним тригонометрические преобразования, которые позволят воспользоваться первым замечательным пределом.
Получим: 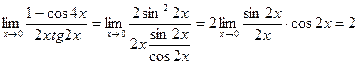 .
.
б) 
Решение. Подстановка х=0 приводит к неопределённости вида  . Положим
. Положим  , тогда 5x=siny,
, тогда 5x=siny,  Ясно, что при
Ясно, что при 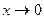 будет
будет  .
.
Придём к пределу:  .
.
Если функция  есть дробь, содержащая иррациональные выражения, то есть радикалы, и непосредственная подстановка при переходе к пределу при х=а приводит к неопределённости вида
есть дробь, содержащая иррациональные выражения, то есть радикалы, и непосредственная подстановка при переходе к пределу при х=а приводит к неопределённости вида  , раскрыть неопределённость часто оказывается возможным, если избавиться от иррациональности в числителе или знаменателе дроби или там и там одновременно.
, раскрыть неопределённость часто оказывается возможным, если избавиться от иррациональности в числителе или знаменателе дроби или там и там одновременно.
в) Найти предел 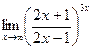 . Чтобы получить в скобках выражение вида
. Чтобы получить в скобках выражение вида  , прибавим и вычтем единицу в числителе дроби:
, прибавим и вычтем единицу в числителе дроби:
 , обозначим 2х-1=у, откуда
, обозначим 2х-1=у, откуда  если
если  , то
, то  . Тогда:
. Тогда:

В решении задачи можно было сделать и такую замену:
 , откуда
, откуда 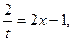

 Если
Если  , то
, то  . Получим:
. Получим: 
г) Найти  .
.
Решение. Пусть -4х=у, тогда  При
При  будет
будет  . Тогда
. Тогда

 , следует заметить, что неопределённости вида
, следует заметить, что неопределённости вида  сводятся различными приёмами к неопределённости вида
сводятся различными приёмами к неопределённости вида  или
или  , раскрытие которых мы уже рассматривали в ряде простых случаев.
, раскрытие которых мы уже рассматривали в ряде простых случаев.
Пример 1.9. а) Вычислить  , при подстановке х=2, получаем
, при подстановке х=2, получаем 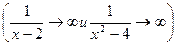 неопределённость вида
неопределённость вида 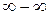 . Преобразуем исходное выражение:
. Преобразуем исходное выражение:
 =
=  .
.
б) Найти  , при
, при 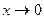 ,
,  ,
, 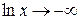 и мы имеем дело с неопределённостью вида
и мы имеем дело с неопределённостью вида  .
.
Преобразуем:  =
=  =(напомним, что
=(напомним, что  , если
, если  (и
(и  ) непрерывны в окрестности точки а) =
) непрерывны в окрестности точки а) =  .
.




