1.1.1Обозначения и термины:
1)  , где
, где  - символ операций (формулы), выполняемых над х для получения соответствующего значения у (Аналитическое задание функции);
- символ операций (формулы), выполняемых над х для получения соответствующего значения у (Аналитическое задание функции);
2)  - область определения функции
- область определения функции  (совокупность значений х, для которой у определена и существует);
(совокупность значений х, для которой у определена и существует);
3)  - область значений функции (совокупность значений у на
- область значений функции (совокупность значений у на  );
);
4) Функция: чётна я, если  ; нечётная, если
; нечётная, если  ; общего вида, если
; общего вида, если  Отметим, что если
Отметим, что если  несимметрична относительно х=0, то функция – общего вида;
несимметрична относительно х=0, то функция – общего вида;
5) Функция периодическая, если существует такое 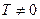 , что
, что 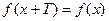 . Т – период функции, наименьшее положительное значение Т – основной период.
. Т – период функции, наименьшее положительное значение Т – основной период.
Пример 1.1. Найти область определения функций:
а)  б)
б)  .
.
Решение. а) Выражение  имеет смысл при
имеет смысл при 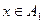 , где
, где  определён для х-2>0, т.е.
определён для х-2>0, т.е.  , где
, где 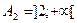 . Числа +3; -3 не входят в область определения данной функции, так как обращают знаменатель
. Числа +3; -3 не входят в область определения данной функции, так как обращают знаменатель  в нуль, поэтому
в нуль, поэтому  , где
, где  . Областью определения заданной функции является пересечение множеств
. Областью определения заданной функции является пересечение множеств 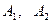 и
и  (см. рис. 1.1)
(см. рис. 1.1)
 |
Рис. 1. 1.
 .
.
б) Действия, указанные формулой  , выполнимы для таких значений х, при которых подкоренное выражение неотрицательно, т.е.
, выполнимы для таких значений х, при которых подкоренное выражение неотрицательно, т.е.  . Решая это неравенство методом интервалов, определяем
. Решая это неравенство методом интервалов, определяем  (см. рис. 1.2).
(см. рис. 1.2).
 |
рис. 1.2
Пример 1.2. Найти область изменения функций:
а)  (локон Аньези); б)
(локон Аньези); б)  .
.
Решение.
а) Очевидно, что 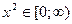 и
и  . Легко видеть, что
. Легко видеть, что  определится как
определится как  .
.
б) Известно, что  , следовательно,
, следовательно,  и
и  определится как
определится как  . (при стремлении
. (при стремлении  к –1 знаменатель положителен и стремится к 0).
к –1 знаменатель положителен и стремится к 0).
Пример 1.3. Определите чётны или нечётны функции:
а) 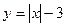 ; б)
; б) 
Решение.
а)  , т.е.
, т.е.  и, в соответствии с определением, функции чётная.
и, в соответствии с определением, функции чётная.
б)  , т.е.
, т.е. 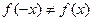 и
и  . Функция общего вида.
. Функция общего вида.
Пример 1.4. Определить периодичность функций (и найти основной период, если он есть): а) 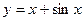 ; б)
; б)  .
.
Решение.
а) В соответствии с определением ищем 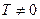 такое, что:
такое, что:  . Раскрыв скобки, получим
. Раскрыв скобки, получим  , откуда
, откуда  .
.  - константа и равенство выполняется для любых х только при
- константа и равенство выполняется для любых х только при  . Функция непериодическая.
. Функция непериодическая.
б) Ищем  из условия
из условия 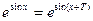 . Логарифмируя, получим
. Логарифмируя, получим  . Известно, что
. Известно, что  - функция периодическая с наименьшим периодом
- функция периодическая с наименьшим периодом  . Следовательно, периодична и наша функция и
. Следовательно, периодична и наша функция и  .
.
1.1.2 Функция 
Как известно из школьного курса математики графиком прямой пропорциональности  является прямая, проходящая через начало координат и составляющая с положительным направлением оси Ох угол
является прямая, проходящая через начало координат и составляющая с положительным направлением оси Ох угол  , где
, где  . Число «k» называют угловым коэффициентом прямой.
. Число «k» называют угловым коэффициентом прямой.
1. Область определения функции  - вся числовая прямая:
- вся числовая прямая:  .
.
2. Область значений – вся числовая прямая  .
.
3. Функция  - нечётная, непериодическая.
- нечётная, непериодическая.
4. 0 (0;0) – точка пересечения прямой с осями координат.
5. Если  , функция возрастает на всей области определения, если
, функция возрастает на всей области определения, если  -убывает на всей области определения.
-убывает на всей области определения.
При 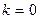 функция постоянна – у=0 (график – ось Ох).
функция постоянна – у=0 (график – ось Ох).
Графики прямых при различных «k» изображены на рис. 1.3
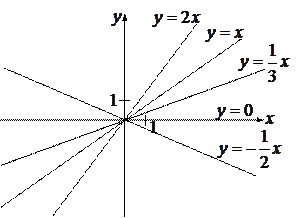 |
Рис. 1.3.
1.1.3 Функция 
Функция вида  ,
,  называется обратной пропорциональностью, её график – гиперболой.
называется обратной пропорциональностью, её график – гиперболой.
1. Функция определена для любого отличного от нуля действительного числа:  . Открытые лучи
. Открытые лучи  - интервалы непрерывности функции.
- интервалы непрерывности функции.
2. Область значений 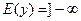 ;
;  .
.
Из пунктов 1 и 2 следует, что гипербола  никогда не пересекает оси координат.
никогда не пересекает оси координат.
3. При  функция убывает на любом интервале непрерывности, располагаясь в 1 и 3 четвертях (рис. 1.4(а)). При
функция убывает на любом интервале непрерывности, располагаясь в 1 и 3 четвертях (рис. 1.4(а)). При  функция возрастает на любом интервале непрерывности, располагаясь во 2 и 4 четвертях (рис. 1.4(в)).
функция возрастает на любом интервале непрерывности, располагаясь во 2 и 4 четвертях (рис. 1.4(в)).
4. Ось Ох – горизонтальная асимптота; ось Оу – вертикальная асимптота графика функции  .
.
5. Функция  - нечётная:
- нечётная:  , поэтому гипербола состоит из двух непрерывных ветвей, симметричных относительно начала координат.
, поэтому гипербола состоит из двух непрерывных ветвей, симметричных относительно начала координат.
Графики обратной пропорциональности при различных коэффициентах «k» изображены на рис. 1.4 (а,в).
 | |||
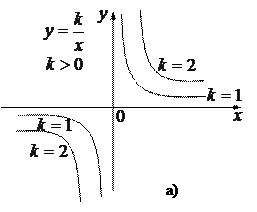 |
Рис.1.4
1.1.4 Функция 
1. Область определения функции  . На всей числовой прямой функция непрерывна.
. На всей числовой прямой функция непрерывна.
2. Область значений функции:  .
.
3. Функция  - чётная:
- чётная:  . Ось Оу является осью симметрии графика функции. Функция
. Ось Оу является осью симметрии графика функции. Функция  непериодическая.
непериодическая.
4. 0 (0;0) – точка пересечения графика функции с осями координат.
5. Если  , то при
, то при  функция убывает, а при
функция убывает, а при  - возрастает. При
- возрастает. При 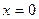 функция достигает своего минимума.
функция достигает своего минимума.
Если  , то при
, то при  функция возрастает, а при
функция возрастает, а при  - убывает. При
- убывает. При 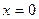 функция достигает максимума. График функции
функция достигает максимума. График функции  называется параболой.
называется параболой.
В точке 0(0;0) функция  достигает экстремума, эта точка называется вершиной параболы.
достигает экстремума, эта точка называется вершиной параболы.
Из п.п.2 и 5 следует, что при  ветви параболы направлены вверх, а при
ветви параболы направлены вверх, а при  - вниз.
- вниз.
На рис. 1.5 изображены параболы при различных «а».
 | |||
 | |||
Рис. 1.5






