Параметрическое задание функции и её дифференцирование.
Пусть даны две функции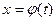 
и 
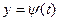одной независимой переменной 
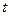, определённые и непрерывные в одном и том же промежутке. Если 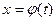монотонна, то обратная к ней функция 
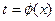однозначна, непрерывна и строго монотонна и 
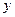можно рассматривать как функцию, зависящую от переменной х посредством переменной 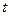, называемой параметром: 
.
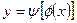В этом случае говорят, что функция 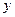от х задана параметрически с помощью уравнений , .
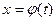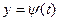Параметрическое задание функций удобно при изучении движения точки. Если точка движется на плоскости, то её координаты х и 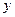являются функциями времени 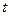. Задав эти функци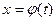и и 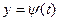, мы полностью определим движение точки.
Так, функция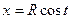 
, 
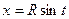
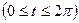задают уравнение окружности радиуса R, с центром в начале координат, а 
, 
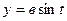
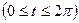- параметрические уравнения эллипса.
Производная функция, заданной параметрическими уравнениям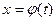и и :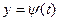
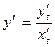
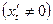
Пример 2.6. Найти 
, если , .
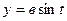Решение: = 
.
Производные высших порядков.
Производной второго порядка от функции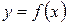 
называется производная от производной первого порядка, то есть 
.
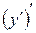Вторая производная обозначается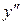 
, или 
, или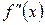 
.
Аналогично производная третьего порядка от функции 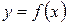есть производная от производной второго порядка 
.
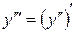Вообще, производная 
порядка от заданной функции 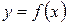есть производная от производной 
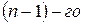порядка и обозначается так: 
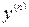, или 
, или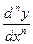 
.
Пример2.7. Найти производные второго порядка функций:
а)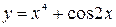 
; б) 
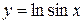в) 
Решение: а)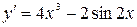 
; 
.
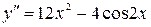б) 
; 
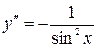
в)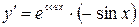 
; 
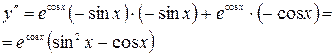
Пример 2.8. Найти производные третьего порядка функций:
а) 
; б)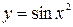 
.
Решение: а) 
; 
; 
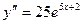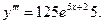
б)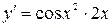 
; 
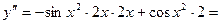
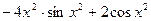
Приложения производной.
Угол между кривыми.
Если две кривые пересекаются в какой-нибудь точке, их направление в этой точке определяется направлением касательных, которые характеризуются угловыми коэффициентам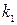и 
и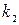 
. Если кривые заданы уравнениям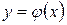и 
и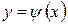 
, то, решая их совместно как систему, можно найти координаты точек пересечения кривых 
, 
,…
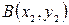Производные функций 
и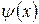 
в точке 
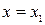численно равны угловым коэффициентам касательных, то есть 
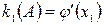и 
.
Вычисление угла между кривыми сводится к вычислению угла между касательными в точке пересечения: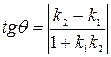 
(3.1)
Пример 3.1. Под каким углом пересекаются парабола 
и окружность 
Решение: 1. Найдем точки пересечения кривых, решив систему уравнений
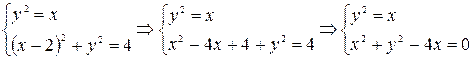
откуда 
и 
, 
.
Подставляя значения этих корней в первое уравнение системы находим:
; 
.
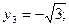
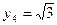Ввиду симметричного расположения кривых относительно оси 
, угол между кривыми в точках 
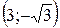и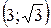 
будет одинаков.
Определим угол между кривыми в точках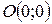 
и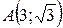 
.
2. Продифференцируем уравнения кривых, как неявные функции. Получим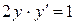 
, откуда 
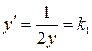и 
, откуда 
.
В точке О оба угловых коэффициента обращаются в бесконечность:
; 
;
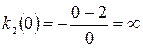это значит, что касательные к обеим кривым в точке О перпендикулярны оси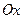 
и угол между ними равен нулю.
В точке А: 
; 
.
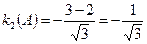Угол между кривыми в точке А находим по формуле (3.1)
, 
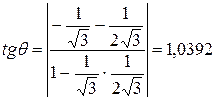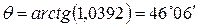
Уравнение касательной и нормали.
Пример 3.2. Составить уравнение касательной и нормали к кривой 
в точке 
.
Решение: Найдем ординату точки касания: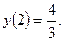 
Для составления уравнений касательной и нормали найдем угловой коэффициент
В точке 
Напомним уравнение касательной 
(3.2)
Откуда 
или 
и уравнение нормали: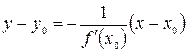 
(3.3)
откуда 
или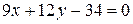 
Приложения производной к задачам механики.
Механический смысл первой производной- скорость движения материальной точки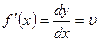 
; механический смысл второй производной
– ускорение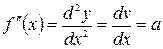 
Пример 3.3. Точка движется по прямой и ее расстояние от начального пункта через 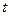равно 
а) В какие моменты точка была в начальной точке?
б) В какие моменты ее скорость равна нулю?
Решение: а) Пребывание в начальной точке означает, что путь равен нулю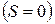 
, т. е.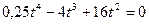 
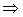
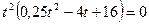
откуда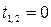 
, 
.
Т.о. точка находится в начальной точке в моменты времен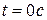и 
и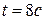 
.
б) Найдем производную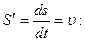 
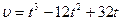
Определяя, в какие моменты времени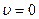 
приходим к уравнению
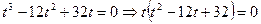откуда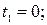 
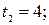
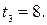
Следовательно, скорость точки равна нулю при 
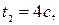
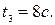
Пример3.4. Круглый металлический диск расширяется от нагревания так, что его радиус равномерно увеличивается на 
С какой скоростью увеличивается его площадь, если радиус равен 
?
Решение: пусть радиус диска равен 
, а площадь 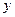. Тогда 
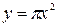, где и 
- функции от времени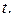 
Дифференцируя по 
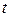обе переменные и , получим две связанные следующим уравнением скорости
Подставляя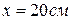 
и 
, найдем скорость увеличения площади диска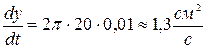 
.
3.2. Дифференциал. Приближенное вычисление функции при помощи дифференциала.
Дифференциалом функции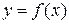 
называется главная часть приращения функции, линейная относительно приращения независимой переменной. Обозначается дифференциал символом 
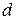. Так как полное приращение функции 
(3.4), где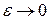 
, то главная часть приращения функции или дифференциал есть первое слагаемое в правой части этого равенства 
Поскольку дифференциал независимой переменной равен ее приращению, то есть 
, то 
Из формулы (3.4) следует, что 
или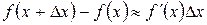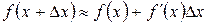 
или 
или 
(3.5)
Формулу (3.5) можно использовать для приближенных вычислений.
Пример 3.5. Вычислить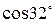 
с точностью до 0,001.
Решение: Примем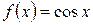 
, тогда 
Положим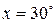 
, 
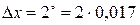(радиан). По формуле (3.5) найдем
Пример 3.6. Вычислить: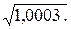 
Решение: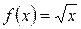 
, 
, 
, 
; 
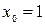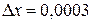
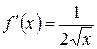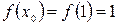
Малые ошибки. Вычисление погрешностей.
Если 
есть погрешность измерения величины , то отношение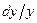 
есть относительная погрешность измерения, а 
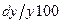есть процентная погрешность измерения.
Пример 3.7. 
Сторона квадрата равна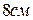 
. На сколько увеличится его площадь, если каждую сторону увеличить на: а) 
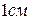; б) 
; в)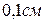 
. Найти главную линейную часть приращения площади этого квадрата и оценить относительную ошибку (в процентах) при замене приращения его главной частью – дифференциалом.
Решение: Пусть сторона квадрата , приращение стороны 
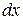. Площадь квадрата 
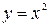. Главная часть приращения площади есть дифференциал 
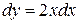. Полагая 
; 
; 
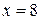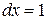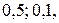найдем соответствующие главные приращения его главные приращения площади:
а)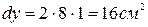 
; б) 
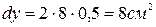; в)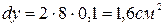 
.
Относительные процентные ошибки получим, составив отношение 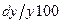с учетом того, что 
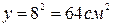. Итак, будем иметь
а)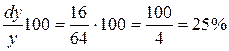 
;
б) 
;
в) 
Сопоставляя результаты, видим, что чем меньше 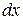, тем правомернее использование дифференциала в приближенных вычислениях.
