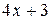Соотношение 
позволяет один из сомножителей подынтегральной функции 
внести под знак дифференциала (если мы знаем его первообразную) и затем применить табличный интеграл.
Пример 7.3.
Подстановка (замена переменной) основана на справедливости соотношения 
(7.1) называемого формулой замены переменной в неопределенном интеграле.
Пример 7.4. 
обозначим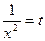 
; Продифференцируем обе части равенства 
и 
Плодотворной в ряде случаев бывает и подстановка вида 
(
непрерывно дифференцируемая функция, имеющая обратную 
).
В этом случае 
и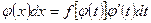 
и если 
, то 
Получаем вторую формулу замены переменной 
(7.2)
Пример 7.5. 
обозначим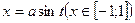 
, 
.
Тогда 
; 
(дифференцируем обе части равенства – каждую по своей переменной). Получаем: 
.
Возвращаясь к исходной переменной получаем (для второго слагаемого)
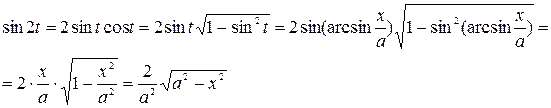
и окончательно: 
.
7.3.Интегрирование выражений, содержащих квадратный трёхчлен.
При интегрировании выражений, содержащих квадратный трёхчлен, главным моментом является выделение полного квадрата:
после этого чаще всего необходимо сделать замену: 
(впрочем, данную замену можно применить и не выделяя полного квадрата).
Пример 7.6. Вычислить интеграл 
.
Решение: 
.
Отметим, что возможные подстановки весьма разнообразны и определяются особенностям задачи.
7.4. Интегрирование рациональных дробей.
Рациональной дробью называется отношение двух многочленов 
(к, n – степени многочленов).
Будем предполагать, что многочлены 
и 
не имеют общих корней.
Рациональная дробь называется правильной, если к<n, и неправильной, если 
.
Если дробь неправильная, то, разделив числитель на знаменатель (по правилу деления многочленов), рациональную дробь можно представить в виде суммы многочлена и правильной дроби:
, 
.
Пример 7.7. 
, т.к.
|
|
- 
Интегрирование многочлена не составляет труда. Рассмотрим интегрирование правильных дробей.
Простейшими дробями называются правильные рациональные дроби следующих видов:
1. 
;
2. 
, 
>1, ( – целое число);
3. 
, где 
, т.е. квадратный трёхчлен 
не имеет вещественных корней;
4. 
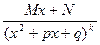, где , >1, ( – целое число).
Вычислим интегралы от простейших дробей. Дроби вида 1 и 2 интегрируются элементарно:
;
.
Для вычисления интеграла от дроби вида 3 представим квадратный трёхчлен в виде 
.
Так как по условию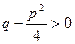 
, обозначим 
и сделаем подстановку 
. Тогда 
. Таким образом, получим
.
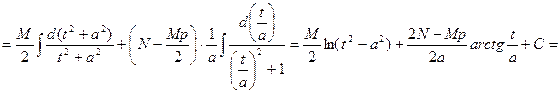
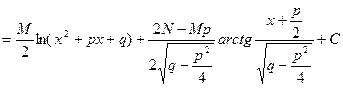Интеграл от дроби вида 4 с помощью несложных преобразований приводится к виду, позволяющему последовательно применять рекуррентную формулу:
(7.1)
Любую правильную дробь единственным образом можно разложить на сумму простейших дробей.
Алгоритм разложения:
1. Привести дробь к правильному виду (далее в данном алгоритме будем рассматривать только правильную дробь).
2. Разложить знаменатель дроби на простейшие множители.
3. Представить дробь в виде суммы всевозможных различных простейших дробей, в знаменателях которых стоят множители знаменателя, а в числителях – соответствующей степени многочлены с неопределёнными коэффициентами.
! Контроль. Число неопределённых коэффициентов должно равняться степени многочлена в знаменателе исходной дроби.
4. Привести сумму простейших дробей к общему знаменателю. Общим знаменателем является знаменатель исходной дроби.
5. Приравнять числители получившейся и исходной дробей, вычислить коэффициенты. Для этого можно воспользоваться двумя способами: 1) приравнять коэффициенты при соответствующих степенях х в многочленах в правой и левой частях равенства; 2) подставить вместо х конкретные числовые значения (в первую очередь – корни знаменателя). Лучше всего комбинировать эти два способа.
Пример 7.8. Вычислить интеграл 
.
Решение:
приравниваем числители
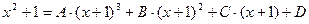
подставим полученные коэффициенты
.
