Пусть функция y = f (x) дифференцируема на интервале (a, b). Тогда существует касательная к графику функции y = f (x) в любой точке M (x; f (x)) этого графика (a < x < b), причем касательная не параллельна оси Оу, поскольку её угловой коэффициент, равный f ¢(x), конечен.
Определение 1: Будем говорить, что график функции у = f (x) имеет на (a, b) выпуклость, направленную вниз – вогнутость (выпуклость, направленную вверх – выпуклость), если он расположен не ниже (не выше) любой касательной к графику функции на (а, b).
Замечание: на участке выпуклости касательные к графику функции не пересекаются с самим графиком и имеют с ним лишь точки касания.
Теорема 1 (признак выпуклости (вогнутости)): Если функция f (х) дважды дифференцируема на интервале (a, b) и f ²(х)≥0 (f ²(х)≤0) на (a, b), то функция f (x) вогнута (выпукла) на (a, b).
Определение 2: Точка М (х 0; f (х 0)) называется точкой перегиба графика функции y = f (x), если в точке М график имеет касательную, и существует такая окрестность точки х 0, в пределах которой график функции y = f (x) слева и справа от точки х 0 имеет разные направления выпуклости.
Теорема 2 (необходимое условие точки перегиба): Если функция f (х) имеет в точке х 0 перегиб и дважды дифференцируема в этой точке, то f ²(х 0)=0.
Замечание: Если в точке х 0 f ²(х 0)=0, то она может и не быть точкой перегиба.
Теорема 3 (достаточное условие перегиба): Пусть функция f (х) дважды дифференцируема в некоторой d -окрестности точки х 0. Тогда, если f ²(x)< f ²(х 0) (f ²(x)> f ²(х 0)) для всех х из (х 0- d, х 0), а f ²(x)> f ²(х 0) (f ²(x)< f ²(х 0)) для всех х из (х 0, х 0+ d), то в точке х0 функция f (х) имеет перегиб, если же f ²(х) во всей d -окрестности точки х 0 имеет один и тот же знак, то в точке х 0 перегиба нет.
Другими словами, если f ²(x) при переходе через точку х 0 меняет знак с «+» на «-», или с «-» на «+», то х 0 — точка перегиба, если же знак f ²(x) в точке х 0 не изменяется, то в точке х 0 перегиба не существует.
Асимптоты.
Определение 1: Если график функции сколь угодно близко приближается к той или иной прямой (при х ®±¥ или вблизи точек разрыва второго рода), то такая прямая называется асимптотой.
Существует три вида асимптот: вертикальные, горизонтальные и наклонные.
Определение 2: Прямая х = х 0 называется вертикальной асимптотой графика функции y = f (x), если хотя бы одно из предельных значений 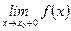 или
или  равно ±¥.
равно ±¥.
Определение 3: Прямая у = а называется горизонтальной асимптотой графика функции y = f (x), при х ®+¥ или х ®-¥, если  или
или  .
.
Определение 4: Прямая у = kx + b называется наклонной асимптотой графика функции y = f (x), при х ®+¥ или х ®-¥, если функцию f (x) можно представить в виде: f (x)= kx + b + a (x), где a (x)®0 при х ®±¥.
Теорема 1: Для того чтобы график функции y = f (x) имел при х ®+¥ или х ®-¥ наклонную асимптоту y = kx + b, необходимо и достаточно, чтобы существовали два предела:

Целесообразно искать асимптоты в следующем порядке:
1) вертикальные асимптоты;
2) горизонтальные асимптоты;
3) наклонные асимптоты.
Исследование функции.
1) найти область определения функции; указать промежутки непрерывности; (по возможности указать область значений функции); найти вертикальные асимптоты;
2) исследовать функцию на чётность, нечётность (в том случае, если область определения симметричное относительное нуля множество), периодичность (в том случае, если функция тригонометрическая);
3) найти точки пересечения графика функции с осями координат;
4) с помощью первой производной исследовать функцию на возрастание, убывание, найти точки экстремума;
5) с помощью второй производной исследовать функцию на выпуклость, вогнутость, найти точки перегиба;
6) найти горизонтальные, наклонные асимптоты;
7) по необходимости найти дополнительные точки графика функции;
8) построить график.
Лекция 12
Первообразная
Восстановление функции по известной производной этой функции составляет одну из основных задач интегрального исчисления.
Определение 1: Функция F (x) называется первообразной для функции f (x) на некотором промежутке X, если для всех значений х из этого промежутка выполняется равенство F ¢(x)= f (x).
Задача отыскания по данной функции f (x) её первообразной решается неоднозначно. Действительно, если F (x) — первообразная для f (x), т. е. F ¢(x)= f (x), то функция F (x)+ C, где С —произвольная постоянная, также является первообразной для f (x), так как [ F (x)+ C ]¢= f (x) для любого числа С.
Теорема 1: Функция, производная которой на некотором промежутке X равна нулю, постоянна на этом промежутке.
Теорема 2: Если F (x) — первообразная для функции f (x) на некотором промежутке X, то любая другая первообразная для f (x) на том же промежутке может быть представлена в виде F (x)+ C, где С — произвольная постоянная.
§43 Неопределённый интеграл.
Определение 1: Если функция F (x) — первообразная для функции f (x), то множество функций F (x) +C, где С — произвольная постоянная, называется неопределённым интегралом от функции f (x)и обозначается символом

При этом функция f(x) называется подынтегральной функцией, f (x) dx — подынтегральным выражением, а переменная х — переменной интегрирования.
Символ  обозначает, таким образом, совокупность всех первообразных для функции f (x).
обозначает, таким образом, совокупность всех первообразных для функции f (x).
Восстановление функции по ее производной или, что то же, отыскание неопределённого интеграла по данной подынтегральной функции называется интегрированием этой функции. Интегрирование представляет собой операцию, обратную дифференцированию. Для того чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.
В связи с понятием первообразной возникает вопрос: для каких функций существуют первообразные (а значит, и неопределённые интегралы).
Доказано любая непрерывная на отрезке функция имеет на этом отрезке первообразную (следовательно, и неопределённый интеграл). В дальнейшем будем считать, что все функции, стоящие под знаком интеграла, непрерывны и формула  имеет смысл.
имеет смысл.
В случае разрывной функции будем рассматривать ее интегрирование только в тех промежутках, в которых она непрерывна.
Геометрически неопределенный интеграл представляет собой множество (семейство) кривых, являющихся графиками первообразных y = F (x)+ С. Если y = F (x) - какая-нибудь кривая, то все другие кривые получаются из неё параллельным сдвигом вдоль оси Оу.
§44 Свойства неопределённого интеграла.
Свойство 1: Производная неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению, т. е.
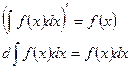
Свойство 2: Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т. е.
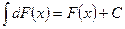
Свойство 3: Постоянный множитель можно вынести из-под знака интеграла, т. е. если k=const¹0,

Свойство 4: Неопределённый интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций отдельно, т. е.
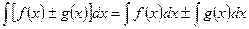 .
.






