Определение 1: Функция f (x) называется непрерывной в интервале (а; b), если она непрерывна в каждой точке этого интервала.
Определение 2: Функция f (x) называется непрерывной на отрезке [ а; b ], если она непрерывна в каждой точке интервала (а; b), и непрерывна в точке а справа, и в точке b слева.
Всякая элементарная функция непрерывна на своей области определения.
Теорема 1: (об устойчивости знака непрерывной функции) Пусть функция f (х) непрерывна в точке х 0 и f (х 0)¹0. Тогда существует d >0 такое, что для всех х Î(х 0- d, х 0+ d) функция f (х) имеет тот же знак, что f (х 0).
Теорема 2: (I теорема Больцано-Коши) Пусть функция f (х) непрерывна на отрезке [ а; b ] и на концах отрезка имеет значения разных знаков. Тогда существует точка с Î(а; b), в которой f (с)=0.
Её геометрический смысл: непрерывная кривая при переходе с одной полуплоскости, границей которой является ось Ох, в другую пересекает эту ось.
Теорема 3: (II теорема Больцано-Коши) Пусть функция f (х) непрерывна на отрезке [ а; b ] причём f (а)= А f (b)= В и А < C < В. Тогда на отрезке [ а; b ] найдётся точка с такая, что f (с)= С.
Её геометрический смысл: непрерывная функция f (х) при переходе от одного значения к другому принимает и все промежуточные значения.
Следствие: Если функция f (х) определена и непрерывна на некотором промежутке Х, то множество её значений Y также представляет некоторый промежуток.
Определение 3: Функция f (x) называется ограниченной на отрезке [ а; b ], если существует число М >0 такое, что для всех х Î[ а; b ] выполняется неравенство | f (x)|£ M.
Теорема 4: (I теорема Вейерштрасса) Если функция f (х) определена и непрерывна на отрезке [ а; b ], то она ограничена на этом отрезке.
Замечание: для интервала (а; b) теорема неверна.
Определение 4: Точной верхней (нижней) гранью функции f (x), определённой на Х, называется наименьшая (наибольшая) из верхних (нижних) граней, ограничивающих Y сверху (снизу).
Теорема 5: (II теорема Вейерштрасса) Если функция f (х) непрерывна на отрезке [ а; b ], то она достигает на этом отрезке своих точных граней, то есть существуют точки х 1, х 2Î[ а; b ] такие что
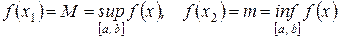
Замечание: после этого можно ввести определения:
Определение 5: Точная верхняя (нижняя) грань функции f (x) называется максимальным (минимальным) значением функции на отрезке.
Теорема 5: (II теорема Вейерштрасса) Непрерывная на отрезке функция имеет на этом отрезке максимальное и минимальное значения.
Теорема 6: (о непрерывности обратной функции) Пусть функция у = f (х) определена, строго монотонна и непрерывна на некотором промежутке Х и пусть Y – множество её значений. Тогда на множестве Y обратная функция х = j (у) однозначна, строго монотонна и непрерывна.
Производная функции.
Пусть на некотором промежутке X определена функция y = f (x). Возьмем любую точку х 0Î Х и зададим аргументу х в точке х 0 произвольное приращение D х такое, что точка х 0+D х также принадлежит X. Функция получит приращение D у = f (х 0+D х)- f (x 0).
Определение 1: Производной функции у = f (x) в точке х 0 называется предел при D х ®0 отношения приращения функции в этой точке к приращению аргумента (при условии, что этот предел существует).
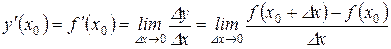
Геометрический смысл производной. Пусть функция y = f (x) определена на интервале (а, b) и пусть точка М на графике функции соответствует значению аргумента х 0, а точка Р - значению х 0+D х. Проведем через точки М и Р прямую и назовем её секущей. Обозначим через j (D х) угол между секущей и положительным направлением оси Ох. Очевидно, что этот угол зависит от D х.
Если существует 
, то прямую с угловым коэффициентом k = tgj 0, проходящую через точку М (х 0; f (x 0)) называют предельным положением секущей МР при D х ®0 (или при Р ® М).
Определение 2: Касательной S к графику функции у = f (x) в точке М называется предельное положение секущей МР при D х ®0 (или при Р ® М).
Итак, производная функции y = f (x) в точке х 0 равна угловому коэффициенту касательной к графику функции y = f (x) в точке М (х 0; f (x 0)) и равна тангенсу угла наклона касательной с положительным направлении оси абсцисс.
Физический смысл производной. Предположим, что функция y = f (x) описывает закон движения материальной точки М по прямой линии, т. е. у = f (х)-путь, пройденный точкой М от начала отсчёта за время х.
Тогда за время х 0 пройден путь y = f (x 0), а за время х 1 - путь y = f (x 1).
За промежуток времени D х = x 1- х 0 точка М пройдёт отрезок пути D y = f (x 1)- f (x 0)= f (x 0+D х)- f (x 0).
Отношение D у /D х называется средней скоростью движения (v ср) за время D х, а предел отношения D у /D х при D х ®0 определяет мгновенную скорость точки в момент времени х 0 (v мгн).
Определение 3: Функция y = f (x) называется дифференцируемой в точке х 0, если её приращение D y в этой точке можно представить в виде D y = А D х + a (D х)D х,
где А - некоторое число, не зависящее от D х, а a (D х) - функция аргумента D х, являющаяся бесконечно малой при D х ®0, т. е. 
. Доказано, что А = f ¢(х 0).
Установим связь между дифференцируемостью функции в точке и существованием производной в той же точке.
Теорема 1: Для того чтобы функция y = f (x) была дифференцируема в точке х 0, необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Таким образом, для функций одной переменной дифференцируемость и существование производной - понятия равносильные. Поэтому операцию нахождения производной часто называют дифференцированием.
Теорема 2: Если функция y = f (x) дифференцируема в данной точке х 0, то она и непрерывна в этой точке.
Замечание. Обратное утверждение неверно. Функция может быть непрерывной в точке, но не быть дифференцируемой, т. е. не иметь производной в этой точке.
