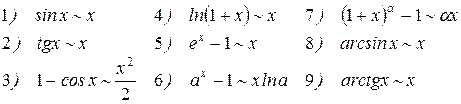Теорема 1: Сходящаяся последовательность имеет только один предел.
Теорема 2: Сходящаяся последовательность ограничена.
Замечание: Ограниченная последовательность может быть расходящейся.
Теорема 3: Сумма (разность, произведение и частное) двух сходящихся последовательностей { хn } и { уn }, есть сходящаяся последовательность, предел которой равен сумме (разности, произведению и частному) пределов последовательностей { хn } и { уn }.
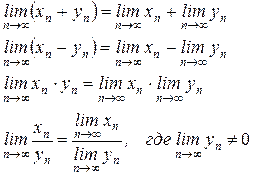
Теорема 4: Если элементы сходящейся последовательности { хn }, начиная с некоторого номера удовлетворяют неравенству хn ³ b (хn £ b), то и предел этой последовательности удовлетворяет неравенству а ³ b (а £ b).
Определение предела функции на языке последовательностей даёт возможность рассматривать теоремы о пределах функций, как и теоремы о пределах последовательностей.
Теорема 5: Пусть функции f (x) и g (x) имеют в точке х 0 пределы В и С. Тогда функции
· f (x)± g (x),
· f (x)· g (x)
· f (x)/ g (x) (при С ¹0)
имеют в точке х 0 пределы, равные соответственно
· В ± С,
· В · С
· В / С.
Следствие: Постоянный множитель можно выносить за знак предела.
Два замечательных предела.
Первый замечательный предел (0/0):
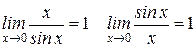
Второй замечательный предел (1¥):
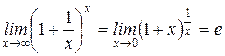
Лекция 8
Бесконечно малые и бесконечно большие функции
Эквивалентные бесконечно малые функции
Непрерывность функции в точке
Бесконечно малые и бесконечно большие функции.
Определение 1: Функция f (x) называется бесконечно малой функцией в точке х = х 0 (или при х ® х 0), если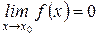 
.
Бесконечно малые функции обладают такими же свойствами, что и бесконечно малые последовательности.
Определение 2: Функция f (x) называется бесконечно большой функцией в точке х = х 0 (или при х ® х 0), если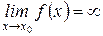 
.
Аналогично определяются бесконечно малые и бесконечно большие функции при х ®¥, х ®+¥, х ®-¥, х ® х 0-0, х ® х 0+0.
Теорема: Функция, обратная бесконечно большой функции является бесконечно малой и наоборот.
Рассмотрим правила сравнения бесконечно малых функций:
Пусть при х ® х 0 функции a (х) и b (х) являются бесконечно малыми. Тогда:
1) если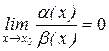 
, то a (х) называется бесконечно малой более высокого порядка, чем b (х);
2) если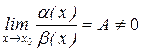 
, то a (х) и b (х) называются бесконечно малыми одного порядка;
3) если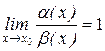 
, то a (х) и b (х) называются эквивалентными бесконечно малыми и обозначается a (х)~ b (х).
4) если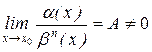 
, то a (х) называется бесконечно малой n -го порядка относительно b (х);
Для бесконечно больших функций имеют место аналогичные правила сравнения.
Эквивалентные бесконечно малые функции.
при х ®0:
