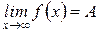Предел числовой последовательности

Определение 1: Число а называется пределом числовой последовательностью { х_n }, если для любого положительного числа e существует номер N такой, что при всех n > N выполняется неравенство | x_n - a |< e. Последовательность { х_n } – называется сходящейся. .

 

Определение 2: Последовательность { х_n } не являющаяся сходящейся называется расходящейся.

 

Из определения 1 предела следует, что каким бы малым мы ни взяли число e >0, начиная с некоторого номера N все элементы последовательности будут отличаться от числа а меньше, чем на e, то есть элементы последовательности неограниченно приближаются к числу а при неограниченном возрастании номера n.

 

Определение 3: Число а не является пределом числовой последовательности { х_n }, если существует положительное число e, что для любого номера N найдётся номер n > N такой, что выполняется неравенство | x_n - a |³ e.

 

Из | x_n - a |< e Þ - e < x_n - a < e Þ а - e < x_n < а + e, то есть элемент x_n находится в e -окрестности точки а.

 

Следствие 1: Пусть { х_n } сходится и имеет своим пределом некоторое число а.

Тогда разность { х_n - а }={ a_n } является бесконечно малой последовательностью, так как для любого e >0 существует номер N такой, что при всех n > N выполняется неравенство | x_n - a |=| a_n |< e.

 

Следствие 2: Всякая бесконечно малая последовательность является сходящейся и имеет своим пределом 0.

 

Следствие 3: Любой элемент x_n сходящейся последовательности, имеющей пределом число а можно представить в виде: x_n = а + a_n, где a_n элемент бесконечно малой последовательности { a_n }. Справедливо и обратное.

 

Определение 4: Число а называется пределом числовой последовательностью { х_n }, если для любой e -окрестности точки а существует номер N такой, что все элементы x_n с номерами n > N находятся в этой e -окрестности.

 

Бесконечно большие последовательности имеют бесконечный предел .

Лекция 7

Предел функции

Основные теоремы о пределах

Два замечательных предела

 

Предел функции.

Определение 1 (по Гейне): Число А называется пределом функции f (х) в точке х = х ₀, если для любой сходящейся к х ₀ последовательности значений аргумента х, отличных от x ₀ соответствующая последовательность значений функции сходится к числу А .

Функция может иметь в точке только один предел.

 

Определение 2 (по Коши): Число А называется пределом функции f (х) в точке х = х ₀, если для любого числа e >0 существует число d >0, такое, что для всех х Î Х, х ¹ х ₀, удовлетворяющих неравенству | x - х ₀|< d, выполняется неравенство | f (x)- A |< e.

 

Теорема 1: Оба определения предела функции эквивалентны.

 

Определение 3 (по Гейне): Число А называется правым (левым) пределом функции f (х) в точке х = х ₀, если для любой сходящейся к х ₀ последовательности значений аргумента элементы которой х_n больше (меньше) х ₀, соответствующая последовательность значений функции сходится к числу А . Определения односторонних пределов.

 

Определение 4 (по Коши): Число А называется правым (левым) пределом функции f (х) в точке х = х ₀, если для любого числа e >0 существует число d >0, такое, что для всех х Î Х, х ¹ х ₀, удовлетворяющих неравенству х ₀< x < х ₀+ d (х ₀+ d < x < х ₀), выполняется неравенство | f (x)- A |< e. Определения односторонних пределов.

 

Теорема 2: Функция f (х) имеет в точке х = х ₀ предел тогда и только тогда, когда в этой точке существует как правый, так и левый пределы и они равны.

 

Определение 5: Число А называется пределом функции f (х) при х ®+¥ (х ®-¥), если для любой бесконечно большой последовательности значений аргумента, элементы х_n которой положительны (отрицательны) соответствующая последовательность значений функции сходится к числу А .

Если пределы функции при х ®+¥ и при х ®-¥ равны , то пишут