Среди корней многочлена могут быть и комплексные.
Теорема 1: Если a= а + ib корень многочлена (r -кратный) с вещественными коэффициентами, то сопряженное комплексное число`a= а - ib, также корень многочлена (r -кратный).
Перемножив два множителя (с сопряжёнными комплексными корнями) получаем:
Таким образом, произведение множителей, соответствующих сопряжённым комплексным корням, можно представить в виде квадратного трёхчлена с вещественными коэффициентами.
Теорема 2: Каждый многочлен с действительными коэффициентами Q (x) может быть представлен в виде произведения множителей с действительными коэффициентами первой и второй степеней соответствующей кратности:
Q (x)= A 0(x - а 1) k 1(x - а 2) k 2…(x - аr) k r(x 2+ p 1 x + q 1) l 1… (x 2+ psx + qs) l s,
где k 1+ k 2+…+ kr +2 l 1+2 l 2+…+2 ls = n.
Лекция 5
Разложение рациональной функции на элементарные дроби
Полярная система координат
Понятие функции
Способы задания функции
Классификация функций
Разложение рациональной функции на элементарные дроби.
Теорема 1: Если рациональная функция 
имеет степень многочлена в числителе меньше степени многочлена в знаменателе, а многочлен Q (x) представим в виде:
Q (x)= А (x - a) r (x - b) s …(x 2+ px + q) t (x 2+ ux + v) l,
то эту функцию можно представить единственным образом в виде:
Данное разложение называется разложением рациональной функции на элементарные дроби.
Метод неопределённых коэффициентов: Умножим обе части разложения на Q (x) и приравняем коэффициенты, стоящие при равных степенях. Решим систему уравнений первой степени.
Теорема 2: Если рациональная функция имеет степень многочлена в числителе не меньше степени многочлена в знаменателе, то выполнив деление получим:
,
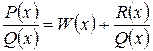где W (x) — некоторый многочлен, а R (x) — многочлен степени меньше, чем Q (x).
Полярная система координат.
Определение 1: Полярная система координат состоит из некоторой точки О - полюса, и исходящего из неё луча ОМ - полярной оси и задаётся единица масштаба для измерения длин отрезков.
Определение 2: Полярными координатами точки М называются числа r и j. При этом число r - полярный радиус, число j - полярный угол. М (r; j), где 0£ r <+¥; и обычно 0£ j £2 p.
Установим связь между полярными координатами точки и ее прямоугольными координатами. Будем предполагать, что точка (0; 0) находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью.
Пусть точка М имеет прямоугольные координаты х и у и полярные координаты r и j
(М (х; у)«М (r; j)), тогда
· 
-выражение прямоугольных координат через полярные;
· 
- выражение полярных координат через прямоугольные.
Понятие функции.
Пусть X и Y —некоторые числовые множества.
Определение 1: Функцией f называется множество упорядоченных пар чисел (х; у) таких, что х Î Х, y Î Y и каждое х входит в одну и только одну пару этого множества, а каждое у входит по крайней мере в одну пару. При этом говорят, что числу х поставлено в соответствие число у и пишут y = f (x).
Определение 2: Число у называется значением функции f в точке х.
Определение 3: Переменную y называют зависимой переменной (или функцией), а переменную х - независимой переменной (или аргументом).
Определение 4: Множество X - область определения (или существования) функции, а множество Y - область значений функции.
Определение 5: Функция, все значения которой равны между собой, называется постоянной. Постоянная функция часто обозначается буквой С (f (x)= C).
На плоскости функцию изображают в виде графика – множеств точек (x; у), координаты которых связаны соотношением у = f (х), называемым уравнением графика.
