Лекция 1
Множества.
Множество действительных чисел.
Виды числовых множеств.
Окрестность точки.
Математический анализ функций одной переменной.
Множества.
В математике все понятия делятся на первичные (основные неопределяемые понятия) и определяемые через первичные или уже известные. Первичными понятиями являются точка, прямая, плоскость и множество. Для всех остальных понятий будут даны определения.
Под множеством понимают совокупность некоторых элементов.
Определение 1: Объекты, из которых состоит множество, называются его элементами или точками. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.
Множества обозначают большими буквами латинского алфавита, а их элементы — малыми буквами.
Если х — элемент множества X, то пишут х Î Х.
Если х не является элементом множества X, то пишут х Ï Х.
Запись Х ={ х 1,..., хn } означает, что множество X состоит из элементов х 1,..., хn. Аналогична запись Х ={ х 1, х 2, х 3,...}.
Например:
· запись А ={0; 1; 25} – означает, что множество А состоит из трёх чисел 0; 1 и 25;
· запись А ={ х: 1< x <25} – означает, что множество А состоит из всех действительных (если не оговорено) чисел, удовлетворяющих двойному неравенству 1< x <25;
· запись А ={ х Î N | 1< x <25} – означает, что множество А состоит из всех натуральных чисел, удовлетворяющих двойному неравенству 1< x <25.
Множество может задаваться:
· путём перечисления его элементов, обычно перечислением задают конечные множества или списком;
· заданием выражением с указанием значений, принимаемых входящими в это выражение переменными;
· путём описания свойств, общих для всех элементов этого множества, и только этого множества. Это свойство называется характеристическим свойством, а такой способ задания множества описанием. Таким образом, можно задавать как конечные, так и бесконечные множества.
Пусть X и Y —два множества.
Определение 2: Множество X содержится в Y (или X есть подмножество множества Y), если в X нет элементов, не принадлежащих Y (Х Ì Y или Y É X (X содержится в Y или Y содержит X).
· знак Ì - строгое включение;
· знак Í - нестрогое включение;
Если не оговорено, есть ли во множестве Y, ещё какие-либо элементы, кроме всех элементов множества X, то употребима запись X Í Y; в противном случае, когда оговорено, что во множестве Y есть ещё другие элементы, кроме всех элементов множества X, употребима запись X Ì Y.
Определение 3: Множества X и Y совпадают, если они состоят из одних и тех же элементов (Х = Y). Другими словами: Множества X и Y равны (совпадают), если Х Ì Y и Y Ì X.
Определение 4: Множество, не содержащее ни одного элемента, называется пустым и обозначается Æ.
Пустое множество является подмножеством любого множества: ÆÌ Х.
При работе в конкретной предметной области обычно ограничиваются некоторой совокупностью объектов.
Определение 5: Зафиксированное каким-либо образом множество объектов, допустимых при данном рассмотрении, называют основным, базовым (универсальным, универсумом) множеством и обозначается U. Или другими словами: все в дальнейшем рассматриваемые (в некотором контексте) множества являются его подмножествами. Данное понятие относительное.
Определение 6: Множество с установленным порядком расположения элементов называют упорядоченным.
Упорядоченное множество в отличие от просто множества записывают внутри круглых скобок.
Множества бывают конечными или бесконечными.
Определение 7: Если число элементов множества конечно — множество называется конечным.
Определение 7: Количество элементов, составляющих множество, называется мощностью множества (численностью, размером, нормой, длиной и др.) и обозначается | А |.
Определение 8: Если между элементами бесконечного множества можно установить взаимнооднозначное соответствие с элементами множества натуральных чисел, то говорят, что множество счётно.
Операции над множествами.
Для визуализации отношений между множествами и операций над множествами обычно используются диаграммы Эйлера-Венна, на которых представлены результаты операций над множествами точек как над геометрическими фигурами на плоскости. Универсальное множество обычно обозначают графически в виде множества точек прямоугольника, а отдельные множества в виде отдельных областей (кругов или овалов) внутри этого прямоугольника.
Определение 1: Объединением (или суммой) двух множеств А и В называется новое множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств, то есть или А, или В:

| 
|
По аналогии с алгеброй чисел объединение иногда называют суммой множеств, так как операция объединения множеств обладает многими свойствами операции сложения чисел.
Определение 2: Пересечением (или произведением) двух множеств А и В называется новое множество, состоящее из элементов, каждый из которых принадлежит обоим этим множествам, то есть и А, и В:

| 
|
По аналогии с алгеброй чисел пересечение иногда называют произведением множеств, так как операция пересечения множеств обладает многими свойствами операции умножения чисел.
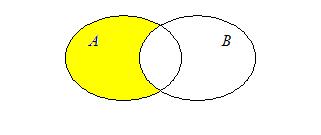
Определение 3: Разностью двух множеств А и В называется новое множество, состоящее из элементов, каждый из которых принадлежит множеству А, но не принадлежит множеству В:

| 
|
Множество А\В называется также дополнением множества В относительно множества А.
Определение 4: Если U – универсальное множество и А Ì U, то разность U\A называется дополнением множества А до множества U, или просто дополнением множества А и обозначается Ā:

| 
|
Определение 5: Симметрической разностью двух множеств А и В называется новое множество, обозначаемое А D В и состоящее из тех и только из тех элементов, которые принадлежат А \ В или В \ А:

| 
|
Пример:
Выписать все подмножества трёхэлементного множества М ={ а, b, c }.
М
 |
{ а, b, c }
 |  |  | |||
{ а, b } { а, c } { b, c }
 |  |  | |||
{ а } { b } { c }
 |  |  | |||
Æ
Определение 6: Алгебра множеств — это непустая система подмножеств (некоторого множества U), замкнутая относительно операций объединения, пересечения, дополнения и симметрической разности.
Например, алгебра натуральных чисел незамкнута относительно вычитания.
В теории алгебры множеств множестваÆ и U играют такую же роль, что и числа 0 и 1 в теории алгебры чисел.
Основные свойства алгебры множеств:
| Объединение È | Пересечение Ç | Разность \ | Симметрическая разность D | |
| Коммутативность | А È В = В È А | А Ç В = В Ç А | ¾ | А D В = В D А |
| Ассоциативность | (А È В)È С = А È(В È С) | (А Ç В)Ç С = А Ç(В Ç С) | ¾ | (А D В)D С = А D(В D С) |
| Дистрибутивность | (А Ç В)È С =(А Ç С)È(В Ç С) | (А È В)Ç С =(А È С)Ç(В È С) | ¾ | ¾ |
| Дистрибутивность | (А \ В)È С =(А \ С)È(В \ С) | (А \ В)Ç С =(А \ С)Ç(В \ С) | ¾ | ¾ |
| А È А = | А Ç А = | А \ А = | А D А =Æ | |
| А È Ā = | А Ç Ā = | А \ Ā = | А D Ā = | |
| Ā È А = | Ā Ç А = | Ā \ А = | Ā D А = | |
| А ÈÆ= | А ÇÆ= | А \Æ= | А DÆ= А | |
| ÆÈ А = | ÆÇ А = | Æ\ А = | ÆD А = А | |
| А È U = | А Ç U = | А \ U = | А D U = | |
| U È А = | U Ç А = | U \ А = | U D А = | |
| U ÈÆ= | U ÇÆ= | U \Æ= | U DÆ= | |
| ÆÈ U = | ÆÇ U = | Æ\ U = | ÆD U = | |
| Законы де Моргана | 
| 
| ¾ | ¾ |

| 
| |||

| ¾ |
Множество действительных чисел.
Рассмотрим аксиоматический метод введения вещественного (действительного) числа.
Множество вещественных чисел разбивается на два множества — Q рациональных и` Q (I) иррациональных чисел.
Определение 1: Рациональным называется число, которое можно представить в виде p / q, где р и q — целые числа, причем q ¹0.
Определение 2: Иррациональным называется всякое вещественное число, которое не является рациональным.
Всякое рациональное число p / q является либо целым, либо его можно представить в виде конечной или периодической бесконечной десятичной дроби.
Всякое иррациональное число представляется непериодической бесконечной десятичной дробью.






