Призма с правильным треугольником в основании

Примечание. Здесь находятся задачи о призмах с правильным треугольником в основании. Если Вы не нашли решение интересующей Вас задачи, пишите об этом на форуме.

Задача.
Площадь боковой поверхности правильной треугольной призмы равна площади основания.Вычислите длину бокового ребра,если сторона основания 7см

Решение.
Площадь правильного треугольника в основании призмы находится по формуле:

По условию задачи a = 7 см
Так как площадь грани призмы в данном случае будет равна 7h, где h - высота бокового ребра, количество граней - три, то

49√3 / 4 = 3 * 7h
49√3 / 4 = 21h
откуда
h = 7√3 / 12

Ответ: длина бокового ребра правильной треугольной призмы равна 7√3 / 12

Задача.
Высота правильной треугольной призмы равна h.
Найдите объем призмы, если диагонали боковых граней, не исходящие из одной точки, перпендикулярны.

Решение.
Поскольку в основании призмі по условию лежит правильный треугольник, то все боковые грани в основании равны. Поскольку диагонали каждой из них пересекаются под прямым углом, то боковые грани представляют собой квадрат. Докажем это.

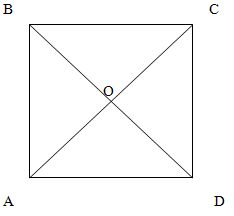
Поскольку AD = BC как основания прямой призмы, углы BOC = AOD как вертикальные, а BCO = OAD, OBC = ODA как внутренние накрест лежащие при параллельных прямых AD и BC. То есть треугольники BOC и AOD равны.

Отсюда следует, что BO = OD, значит треугольники BOC и COD также равны, у них смежная сторона OC, а углы COB = COD = 90 градусам. Из этого следует, что CD =BC = AD = AB.

ABCD - квадрат

Следовательно, объем призмы будет равен
V = Sh

Площадь основания - правильный треугольник. Откуда
S = √3/4 h²
V = √3/4 h³

Ответ: √3/4 h³.

Призма с правильным треугольником в основании (часть 2)

Задача.
Найти площадь правильной треугольной призмы, сторона основания которой 6 см, а высота - 10 см.

Решение.
Площадь правильного треугольника в основании призмы находится по формуле:

По условию задачи a = 6 см откуда S = √3 / 4 * 36 = 9√3

Поскольку у правильной треугольной призмы оснований два, то площадь оснований будет равна
9√3 * 2 = 18√3

Площадь каждой из граней будет равна 6 * 10 = 60, а поскольку граней три, то 60 * 3 = 180

Таким образом, площадь полной поверхности призмы будет равна 180 + 18√3 ≈ 211, 18 см кв.

Ответ: 180 + 18√3 ≈ 211,18

Призма с треугольником в основании

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме.

Задача

В основании прямой призмы лежит прямоугольный треугольник с катетами 7 и 8.Боковые ребра равны 8/п. Найдите объем цилиндра описанного около этой призмы.

Решение.
Найдем диагональ основания призмы, исходя из информации о размере ребер ее основания.

По теореме Пифагора, найдем квадрат гипотенузы треугольника, лежащего в основании.
7² + 8² = 113

Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).
У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.

Таким образом, цилиндр, описанный около заданной призмы, будет иметь диаметр, равный гипотенузе прямоугольного треугольника, лежащего в основании призмы и высоту, равную высоте призмы. Таким образом, объем цилиндра составит:

V= пr²h, где
п - число пи
r - радиус основания цилиндра
h - высота цилиндра

Поскольку гипотенуза прямоугольного треугольника, лежащего в основании призмы одновременно является диаметром цилиндра, описанного вокруг призмы, то радиус цилиндра будет равен половине гипотенузы, то есть квадратный корень из 113 деленный пополам, а квадрат радиуса, соответственно равен r²=113/4.

По условию задачи высота ребра призмы равна 8/п.
Таким образом:

V=п*113/4*8/п
V=226

Ответ: 226

Задача

Основанием прямой призмы является равнобедренный треугольник, в котором высота проведенная к основанию равняется 8см.Высота призмы равняется 12см. Найдите полною поверхность призмы если боковая грань что содержит основание треугольника - квадрат.

Решение.
Площадь поверхности призмы будет равна сумме площадей оснований и сумме площадей боковых поверхностей, то есть

S = 2S₁ + S₂ + 2S₃, где S₁ - площадь основания призмы, S₂ - площадь боковой поверхности, содержащей основание, S₃ - площадь боковой поверхности, содержащей стороны равнобедренного треугольника. (Они равны, так как стороны основания равны в следствие того, что треугольник равнобедренный, а вторые стороны равны высоте призмы)

Поскольку боковая грань, содержащая основание треугольника, является квадратом, то основание треугольника также равно 12 см. (основание треугольника одновременно является стороной грани).

Таким образом, зная высоту и основание равнобедренного треугольника можно найти его остальные стороны и площадь.

S₁ = 1/2ah = 1/2 * 12 * 8 = 48 см².

Катеты, соответственно равны (у нас высота, являющаяся в равнобедренном треугольнике одновременно и медианой 12 /2 = 6 см, с каждым из катетов образует прямоугольный треугольник) по теореме Пифагора

sqrt(6² + 8²) = 10 см

Таким образом

S₂ = 12 * 12 = 144 см².
S₃ = 10 * 12 = 120 см².

S = 2S₁ + S₂ + 2S₃ = 2 * 48 + 144 + 2 *120 = 480 см².

Ответ: 480 см².

Призма с треугольником в основании (часть 2)

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о призме). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√".

Задача

Площадь боковой поверхности правильной треугольной призмы равна площади основания. Вычислите длину бокового ребра, если сторона основания 7см.

Решение.
Площадь правильного треугольника, который является основанием правильной треугольной призмы, найдем по формуле:
S = a²√3 / 4
S = 49√3 / 4

Площадь боковой поверхности правильной треугольной призмы найдем по формуле
S = 3 ab
тогда
S = 3 * 7 * b = 21b

Таким образом,
49√3 / 4 = 21b
b = 49√3 / 84
b = 7√3 / 12

Ответ: 7√3 / 12

Задача

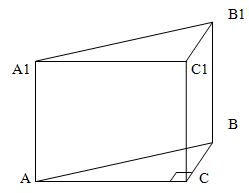
В основании прямой треугольной призмы лежит прямоугольный треугольник с катетами 8 и 6 см. Найти боковое ребро призмы, если ее боковая поверхность равна 120 квадратных сантиметров.

Решение.
Сначала найдем гипотенузу основания призмы.

AB² = AC² + BC²
AB² = 8² + 6²
AB² = 64 + 36
AB = √100
AB = 10

Обозначим боковое ребро призмы как h. Боковое ребро одновременно является и высотой призмы, поскольку по условию задачи призма является прямой. Тогда площадь боковой поверхности призмы является суммой площадей трех прямоугольников - ACC1A1, CBB1C1 и ABB1A1 или, если подставить известные значения катетов основания призмы, то

10h + 6h + 8h = 120
24h = 120
h =5

Ответ: ребро прямоугольной призмы с прямоугольным треугольником в основании равно 5 см.

Призма с треугольником в основании (часть 3)

Задача.
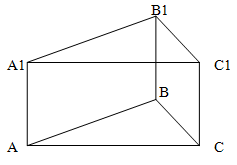
Основание прямой призмы - треугольник со сторонами 5 и 3 см и углом 120 градусов между ними. Наибольшая из площадей боковых граней равна 35 см2, найти площадь боковой поверхности.

Решение.
Согласно теореме косинусов

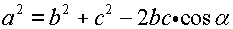
Откуда
AC² = AB² + BC² - 2*AB*BC*cos 120
AC² = 25 + 9 - 2*5*3*cos 120

Косинус 120 градусов найдем по таблице значений тригонометрических функций.
AC² = 34 - 30 (-0.5)
AC² = 49
AC = 7

Каждая из граней боковой поверхности представляет собой прямоугольник. При чем длина одной из сторон прямоугольников одинакова и равна высоте призмы. Таким образом, боковая грань призны наибольшей площади лежит на той стороне основания, длина стороны которого наибольшая.

То есть наибольшая из боковых граней имеет длину основания 7 см.
Откуда высота призмы равна 35 / 7 = 5 см

Таким образом, площадь боковой поверхности будет равна сумме площадей каждой из боковых граней

S = 5*5 + 3*5 + 7*5 = 75 см²

Ответ: 75 см².