Задача
В прямоугольнике CKMN проведена биссектриса угла C,которая пересекает сторону KM в точке E, причём длина отрезка KE на 3 см меньше длины ME. Найдите MN, если периметр CKMN равен 51 см.
Решение.
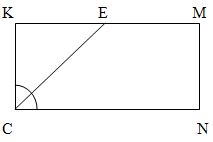
Поскольку CE - биссектрисса угла С, то угол KCE равен 90 / 2 = 45 градусов.
Тогда в прямоугольном треугольнике CKE угол KEC найдем исходя из того, что сумма углов треугольника равна 180 градусам. Поскольку два угла из трех нам известны (К - прямой угол прямоугольника, угол KEC равен 45 градусам), то 180 - 90 - 45 = 45 градусов.
Поскольку два угла треугольника CKE равны между собой, то этот прямоугольный треугольник также является и равнобедренным. Исходя из этого CK=KE=MN.
Обозначим длину отрезка KE как x. Тогда EM будет равно х+3. Таким образом, периметр прямоугольника будет равен
2 (CK + KE + EM) = 51
Учтем, что CK = KE
2 (x + x + x + 3) = 51
2(3x + 3) = 51
6x + 6 = 51
6x = 45
x = 7,5 см
Так как KE = CK = MN, то MN = 7,5 см
Ответ: 7,5 см
Периметр и стороны прямоугольника
Периметр и стороны прямоугольника
Задача
Периметр прямоугольника равен 32 сантиметрам, а сумма площадей квадратов, построенных на каждой из его сторон - 260 квадратных сантиметров. Найдите стороны прямоугольника.
Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=32
Сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, четыре) будет равна
2x2+2y2=260
Решаем полученную систему уравнений. Из первого уравнения выводим, что
x+y=16
x=16-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
2(16-y)2+2y2=260
2(256-32y+y2)+2y2=260
512-64y+4y2-260=0
4y2-64y+252=0
Решаем полученное квадратное уравнение.
D=4096-16x252=64
x1=9
x2=7
Теперь примем во внимание, что исходя из того, что x+y=16 (см. выше) при x=9, то y=7 и наоборот, если x=7, то y=9
Ответ: Стороны прямоугольника равны 7 и 9 сантиметров
Задача
Периметр прямоугольника 26 см, а сумма площадей квадратов, построенных на двух его смежных сторонах, равна 89 кв. см. Найдите стороны прямоугольника.
Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=26
Сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, два и это квадраты ширины и высоты, поскольку стороны смежные) будет равна
x2+y2=89
Решаем полученную систему уравнений. Из первого уравнения выводим, что
x+y=13
y=13-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
(13-y)2+y2=89
169-26y+y2+y2-89=0
2y2-26y+80=0
Решаем полученное квадратное уравнение.
D=676-640=36
x1=5
x2=8
Теперь примем во внимание, что исходя из того, что x+y=13 (см. выше) при x=5, то y=8 и наоборот, если x=8, то y=5
Ответ: 5 и 8 см
Задача
Найти площадь прямоугольника если его периметр равен 26 см а стороны пропорциональны как 2 к 3.
Решение.
Обозначим стороны прямоугольника через коэффициент пропорциональности x. Тогда:
2(2x+3x)=26
2x+3x=13
5x=13
x=13/5
Теперь, исходя из полученных данных, определим площадь прямоугольника:
2x*3x=2*13/5*3*13/5=40,56 см2
Площадь прямоугольника
Примечание. Это часть курса обучения с задачами по геометрии (раздел прямоугольник). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
Задача.
Длина прямоугольника увеличена на 25%. На сколько процентов надо уменьшить ширину, чтобы его площадь не изменилась?
Решение.
Площадь прямоугольника равна
S = ab
В нашем случае один из множителей увеличился на 25%, что означает a2 = 1,25a. Таким образом, новая площадь прямоугольника должна быть равна
S2 = 1,25ab
Таким образом, для того, чтобы вернуть площадь прямоугольника к начальному значению, то
S2 = S / 1.25
S2 = 1,25ab / 1.25
поскольку новый размер а изменять нельзя, то
S2 = (1,25a) b / 1.25
1 / 1,25 = 0,8
Таким образом, величину второй стороны нужно уменьшить на (1 - 0,8) * 100% = 20%
Ответ: ширину нужно уменьшить на 20%.
Тригонометрия
Таблица значений тригонометрических функций
Примечание. В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби - символ "/".
Для определения значения тригонометрической функции, найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов - ищем строку с заголовком sin (синус) и находим пересечение этой строки со столбцом "30 градусов", на их пересечении считываем результат - одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов и т.д.
| значение угла α (градусов) | |||||||||||||
| значение угла α в радианах | π/12 | π/6 | π/4 | π/3 | 5π/12 | π/2 | 2π/3 | 3π/4 | 5π/6 | π | 3π/2 | 2π | |
| sin (синус) | 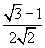
| 1/2 | √2/2 | √3/2 | 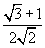
| √3/2 | √2/2 | 1/2 | -1 | ||||
| cos (косинус) | 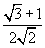
| √3/2 | √2/2 | 1/2 | 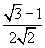
| -1/2 | -√2/2 | -√3/2 | -1 | ||||
| tg (тангенс) | 2 - √3 | 1/√3 | √3 | 2 + √3 | - | -√3 | -1 | -√3/3 | - | ||||
| ctg (котангенс) | - | 2 + √3 | √3 | 1/√3 | 2 - √3 | -√3/3 | -1 | -√3 | - | - | |||
| sec (секанс) | 2/√3 | √2 | - | -√2 | -1 | - | |||||||
| cosec (косеканс) | - | √2 | 2/√3 | √2 | - | -1 | - |
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения.






