Задача.
Точка A находится на расстоянии 1 см до одной из двух перпендикулярных плоскостей.
Найдите расстояние от точки A до второй плоскости, если расстояние от A до прямой их пересечения равно √5 см.
Решение.
Проведем перпендикуляр от точки А также и ко второй плоскости. Перпендикуляры к плоскостям от точки А, а также расстояния от них до прямой пересечения плоскостей образуют прямоугольник, диагональ которого является расстоянием от точки А до прямой пересечения плоскостей и равна по условию √5 см.
Поскольку длина одного перпендикуляра, являющегося стороной прямоугольника, нам известна, то длину второго перпендикуляра найдем как сторону прямоугольника:
х2 + 1 = 5
х2 = 4
x = 2
Ответ: расстояние от точки А до второй плоскости равно 2 см.
Прямые на плоскости
Примечание. Это часть урока с задачами по геометрии (раздел прямые на плоскости). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме.
Задача
Две прямые а и в пересекаются в точке О.Докажите,что все прямые,которые проходят не через точку О и пересекают каждую из данных прямых, лежат в одной плоскости.
Доказательство.
Пусть прямая, не пересекающая точку О пересекает каждую из данных прямых. Поскольку обе данные прямые лежат в одной плоскости, то все точки, принадлежащие данным прямым, равно как и точки пересечения с третьей прямой лежат в одной плоскости.
Воспользуемся аксиомой стереометрии:
"Если две точки прямой лежат на одной плоскости, то все точки данной прямой лежат в этой плоскости. "
Откуда проведенная нами прямая также лежит в данной плоскости.
Точка и плоскость
Задача.
Расстояние от некоторой точки до плоскости квадрата равно 4 см, а до каждой из его сторон 6 см.
Найдите диагональ квадрата.
Решение.
Расстояния от точки до углов квадрата образуют правильную пирамиду.

Таким образом, OKC является прямоугольным треугольником. Откуда
KC2 + OK2 = OC2
KC2 = OC2 - OK2
KC2 = 36 - 16
KC = √20 = 2√5
Откуда диагональ квадрата равна KC * 2 = 4√5
Ответ: 4√5
Задача.
Из O -центра равностороннего треугольника ABC проведен перпендикуляр OM к плоскости треугольника ABC.
Найдите длину OM, если BC=6см, а MC=4см.
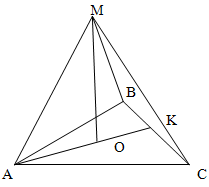
Решение.
Точка М вместе с правильным треугольником образует правильную пирамиду, поскольку ее вершина проецируется в центр основания.
МОС - прямоугольный треугольник. Поскольку ABC - правильный треугольник, а О - является его центром, то OC будет равно длине радиуса описанной окружности. Длину радиуса описанной окружности найдем как
R = a √3 / 3
OC = BC√3 / 3
OC = 6√3 / 3 = 2√3
Откуда
OM2 + OC2 = MC2
OM2 = MC2 - OC2
OM2 = 16 - 12
OM = 2
Ответ: 2 см






