Задача.
В параллелограмме меньшая высота и меньшая сторона равны 9 см и корню из 82 соответственно.Большая диагональ 15 см.Найти площадь параллелограмма.
Решение.
Обозначим меньшую высоту параллелограмма ABCD, опущенную из точки B на большее основание AD как BK.
Найдем значение катета прямоугольного треугольника ABK, образованного меньшей высотой, меньшей стороной и частью большего основания. По теореме Пифагора:
AB2 = BK2 + AK2
82 = 92 + AK2
AK2 = 82 - 81
AK = 1
Продлим верхнее основание параллелограмма BC и опустим на него высоту AN из его нижнего основания. AN = BK как стороны прямоугольника ANBK. У получившегося прямоугольного треугольника ANC найдем катет NC.
AN2 + NC2 = AC2
92 + NC2 = 152
NC2 = 225 - 81
NC2 = √144
NC = 12
Теперь найдем большее основание BC параллелограмма ABCD.
BC = NC - NB
Учтем, что NB = AK как стороны прямоугольника, тогда
BC = 12 - 1 = 11
Площадь параллелограмма равна произведению основания на высоту к этому основанию.
S = ah
S = BC * BK
S = 11 * 9 = 99
Ответ: 99 см2.
Задача
В параллелограмме АВСД на диагональ АС опущен перпендикуляр ВО. Найдите площадь параллелограмма, если АО=8, ОС=6 и ВО=4.
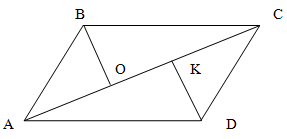
Решение.
Опустим на диагональ АС дополнительно еще один перпендикуляр DK.
Соответственно, треугольники AOB иDKC, COB и AKD попарно равны. Одна из сторон является противолежащей стороной параллелограмма, один из углов - прямой, так как является перпендикуляром к диагонали, а один из оставшихся углов является внутренним накрест лежащим для параллельных сторон параллелограмма и секущей диагонали.
Таким образом, площадь параллелограмма равна площади указанных треугольников. То есть
Sпаралл = 2SAOB +2SBOC
Площадь прямоугольного треугольника равна половине произведения катетов. Откуда
S = 2 (1/2 8 * 4) + 2 (1/2 6 * 4) = 56 см2
Ответ: 56 см2.
Высота параллелограмма
Примечание. Это часть урока с задачами по геометрии (раздел параллелограмм). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме.
См. также: Свойства и площадь параллелограмма.
Задача.
| Висота паралелограма проведена з вершини тупого кута і дорівнює 5 см. Висота ділить сторону парелелограма навпіл. Гострий кут паралелограма доривнюе 30 градусів. Знайдіть діагональ паралелограма, проведену з вершини тупого кута, и кути, яки вона утворює зі сторонами паралелограма. | Высота параллелограмма проведена из вершины тупого угла и равняется 5 см. Высота делит сторону параллелограмма пополам. Острый угол равняется 30 градусам. Найдите диагональ параллелограмма, проведенную из вершины тупого угла и углы, которые она образует со сторонами параллелограмма. |
Решение.
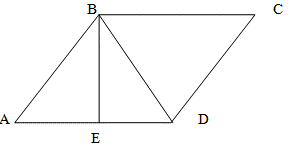
Поскольку, по условию задачи, AE=ED, то треугольники ABE и DBE равны между собой (по первому признаку равенства треугольников: равны две стороны и угол между ними, AE=ED и BE - общая сторона, а BE образует с AD угол 90 градусов). Таким образом, угол ADB равен 30 градусам. Соответственно, угол DBC также равен 30 градусам как внутренние накрест лежащие при параллельных прямых BC и AD.
Из прямоугольного треугольника ABE определим, что угол ABE равен 180 - 90 - 30 = 60 градусов. Откуда (из равенства треугольников ABE и DBE) угол EBD также равен 60 градусов. Таким образом, диагональ образует со вторым основанием угол ABD = 60 + 60 = 120 градусов. BDC = ABD = 120 градусов как внутренние накрест лежащие.
Найдем длину диагонали.
BE / BD = cos ∠EBD
BE / BD = cos 60
Подставим значение косинуса 60 градусов и получим:
BE / BD = 1/2
По условию задачи BE = 5 см, откуда
5 / BD = 1/2
BD = 10
Ответ: длина диагонали параллелограмма равна 10 см, углы, которые образует диагональ с основаниями равны 30 и 120 градусов.
Прямоугольник
Периметр прямоугольника






