Пусть в пространстве заданы две совершенно произвольные аффинные системы координат с общим началом, R = { O, , , } и R ¢ = { O, , , } – реперы, с помощью которых они определяются. Пусть – произвольный вектор, (x 1, x 2, x 3) – его координаты в первой СК, (, x 2¢, x 3¢) – во второй. Будем называть (x 1, x 2, x 3) старыми координатами вектора, а (, x 2¢, x 3¢) – новыми его координатами.
Найдем связь между этими координатами. Пусть нам известно разложение базисных векторов второго базиса B ¢ = { , , } по первому базису B = { , , } :
= с 11 + с 21 + с 31,
= с 12 + с 22 + с 32, (20)
= с 13 + с 23 + с 33.
Составим из коэффициентов этого разложения матрицу, выписывая коэффициенты разложения из каждой строки в столбец с тем же номером:
с 11 с 12 с 13
С = с 21 с 22 с 23
с 31 с 32 с 33 .
Эта матрица называется матрицей перехода от первого базиса ко второму. Имеем:
= x 1 + x 2 + x 3
= x 1¢ + x 2¢ + x 3¢.
Подставим в последнее равенство выражения (20):
= x 1¢ (с 11 + с 21 + с 31) + x 2¢ (с 12 + с 22 + с 32 ) + x 3¢ (с 13 + с 23 + с 33 ).
Раскроем скобки и сгруппируем коэффициенты при одинаковых векторах:
= (с 11 x 1¢ + с 12 x 2¢ + с 13 x 3¢) + (с 21+ с 22 x 2¢ + с 23 x 3¢) + (с 31+ с 32 x 2¢ + с 33 x 3¢).
Сравниваем с (*), и в силу единственности разложения вектора по базису, получаем
x 1= с 11 x 1¢ + с 12 x 2¢ + с 13 x 3¢,
x 2 = с 21+ с 22 x 2¢ + с 23 x 3¢, (21)
x 3 = с 31+ с 32 x 2¢ + с 33 x 3¢.
Если использовать столбцы, составленные из координат
x 1 x 1¢
X = x 2 X ¢= x 2¢
x 3, x 3¢,
То систему (21) можно переписать в виде одного матричного равенства:
X = CX ¢ (21¢)
Þ X ¢= C –1 X,(22)
т.е. для того, чтобы найти новые координаты вектора по старым, необходимо выписать формулы, аналогичные (21), только в качестве коэффициентов будут использованы элементы матрицы C –1, а штрихи у координат будут стоять в левых частях равенств. Можно решить систему уравнений (21) относительно неизвестных x 1¢, x 2¢, x 3¢ и мы получим те же формулы.
К сожалению, не всегда к моменту изучения этого параграфа студенты успевают пройти по алгебре произведение матриц и обратную матрицу. Но ко времени экзамена этот материал обязательно должен быть пройден. Необходимые пояснения будут даны на практических занятиях по геометрии.
Координаты точки совпадают с координатами ее радиус-вектора, поэтому они пересчитываются по тем же формулам (21¢) и (22). Заметим, что все рассуждения, приведенные при выводе формул (17) и (17¢) верны и для произвольной аффинной СК. Поэтому в случае переноса начала координат в точку O ¢(a, b, c) координаты точки пересчитываютcя по формулам
x 1= x 1¢ + a, x 1¢ = x 1 – a,
x 2 = x 2¢ + b, (22) x 2¢ = x 2 – b, (22¢)
x 3 = x 3¢ + c. x 3¢ = x 3 – c.
Все сказанное выше верно и для преобразования аффинной СК на плоскости.
Примеры решения задач.
1. ABCD – параллелограмм, O – его центр, M, N, P, Q – середины сторон AB, BC, CD, DA соответственно. Векторы = и = выбраны в качестве базисных. Найти координаты вектора в базисе {, }.
Решение. По правилу треугольника = + ; =, а по
правилу параллелограмма сложения векторов = + = +. Поэтому = (+) + = + . Значит,.
Ответ:.
2. Даны координаты векторов (17, 0) и (–1, 1) в ортонормированном базисе. Найти такое l, при котором вектор = +l имеет абсолютную величину | | = 25 (если решений два, то достаточно взять одно из них). Найти единичный вектор, коллинеарный.
Решение. Вектор = +l· имеет координаты (17 – l, 0 + l). Находим его длину и приравниваем ее к 25. Получаем квадратное уравнение относительно неизвестного l:
(17 – l)2 + l2 = 625,
2l2 – 34l + 289 = 625 Û 2l2 – 34l – 336 = 0, Û
Û l2 – 17l – 168 = 0.
Решая его, находимl1 = – 7;l2= 24.Поскольку по условию достаточно найти только одно решение, ограничиваемся l1= – 7.Тогда находим координаты вектора (24, 7). И, чтобы получить единичный вектор ||, мы делим координаты вектора на длину этого вектора, т.е. на 25:.
Ответ: l1= – 7,.
3. Даны координаты вектора (–2, –2) в декартовой системе координат. Вычислить координаты вектора, полученного из поворотом: a) на угол a = 120o, б) на угол b = 90°. Пусть =. Вычислить полярные координаты точки A, если полярная ось совпадает с Ox.
Решение. Координаты вектора (x ¢, y ¢), полученного из вектора (x, y) поворотом на угол a, вычисляются по формулам:
x ¢= x ·cos a – y ·sin a,
y ¢= x ·sin a + y ·cos a.
(Не путать с формулами, по которым изменяются координаты данного вектора при повороте координатных осей!)
а) В нашем случае имеем cos a = –, sin a =.
x ¢= – (–2) + 2· = 2,
y ¢= –2·– 2·(–) = –2.
б) Имеем sin 90°=1; cos 90°= 0 и по тем же формулам находим (2,–2).
Если известны декартовы координаты точки А (x, y), то ее полярные координаты (r, φ) находятся по формулам:
r =,
cos j =, sin j =.
Декартовы координаты точки А совпадаютс координатами ее радиус-вектора. Поэтому А (–2,–2). Отсюда находим r = 4; cos j = – ; sin j = – .Значит j =. А (4, ).
Ответ: а) (2,–2); б) (2,–2); А (4, ).
4. Даны координаты двух вершин A (3,-2), B (8, 5) квадрата ABCD. Найти координаты двух других вершин.
Решение. Находим (5, 7). Вектор может быть получен из поворотом на 90о, либо на –90о. Таким образом, задача имеет два решения.
Так же, как и в предыдущей задаче находим, что (–7, 5), либо (7,–5). Для того, чтобы найти координаты точки D надо к координатам точки A прибавить координаты вектора: D (- 4, 3). Далее используем, что = и находим координаты C (1, 10). Второй ответ ищется аналогично.
Ответ: C (1, 10), D (– 4, 3), C ¢(15, 0), D ¢(10,–8).
5. Вершины четырехугольника находятся в точках A (1, 2), B (7,– 6), C (11,–3), D (8, 1). Показать, что ABCD – трапеция. Найти длины оснований трапеции, ее площадь и cosÐ DAB.
Решение. Находим координаты векторов (6,–8), (4, 3), (–3, 4), (7,–1). Проверяем векторы, определяемые противоположными сторонами четырехугольника на коллинеарность:
– = – – верно, значит коллинеарен.
= – неверно, значит неколлинеарен.
Таким образом, в четырехугольнике две противоположные стороны коллинеарны, а две – нет. Значит это – трапеция, и основаниями являются AB и CD. Находим длины сторон:
½½ = = 10,
и аналогично ½½= 5; ½½=5; ½½= 5.
Обозначим a =Ð BAD.
cos a = = =,
следовательно Ð BAD = 45o. Не во всех вариантах может получиться табличный угол, поэтому далее действуем так: зная cos a,находим
sin a = =.
Tогда h =½½· sin a = 5. Зная высоту и длины оснований находим площадь: S =(AB + CD)· h =.
Ответ: ½½ = 10, ½½= 5, cos a =, SABCD =.
6. Дано ½½= 10, ½½ = 3, a =Ð(, ) = 30o. Найти площадь треугольника, построенного на векторах = – 3 и = 2 + 5, отложенных из одной точки. Найти длину медианы, исходящей из этой же точки.
Решение. Площадь параллелограмма построенного на векторах и , численно равна модулю их векторного произведения. Площадь треугольника, построенного на этих векторах равна половине площади параллелограмма: SΔ= ½ ´ ½. Пользуясь свойствами и определением векторного произведения находим
½ ´ ½=½( – 3 )´(2 + 5 )½=½ ´ + 5 ´ – 3´ – 15 ´ ½=
=½ + 5 ´ + 3 ´ +15½= 8½ ´ ½= 8½½·½½·sin a =
= 8·10·3· = 120.
SΔ= ½ ´ ½= 60 .
Если AD – медиана D ABC, то = (+). В нашем случае, если
– вектор, задающий медиану, то = ( + ) = +.
Нам требуется найти длину этого вектора. Самое первое следствие из определения скалярного произведения: скалярный квадрат вектора 2 = · равен квадрату его длины ½½2. Имеем
½½2= · = ( + )·(+ ) = 2 + 3 · + 2=
= ½½2+ 3½½·½½ · cos a +½½2 =
= ·100 + 3·10·3· + 9 = 234 + 45.
Значит, ½½ =.
Ответ: S Δ= 60, длина медианы равна.
Подчеркнем, что ни в коем случае нельзя использовать обозначение 2 вместо ´; 2означает ·. Особо обращаем внимание, что при решении использовалось свойство ´ = – ´ .
7. Докажите, что векторы (10, 11, 2) и (10,–10, 5) отложенные из одной точки, можно взять в качестве ребер куба, и найдите третье ребро куба, исходящее из этой же точки.
Решение. Для того, чтобы векторы и могли служить ребрами куба, они должны быть друг другу перпендикулярны и иметь одинаковую длину. Проверяем:
· = 10·11 + 11·(–10) + 2· 5 = 0 Þ ^ ,
| | = = 15,
| | = = 15.
Вектор, задающий третье ребро куба, должен быть перпендикулярен и и должен иметь одинаковую с ними длину.
Согласно определению векторного произведения вектор ´ будет перпендикулярен и. Выясним, какую он будет иметь длину:
½ ´½=½½ · ½½ × sinÐ( , ) = 15·15· sin 90o= 225.
Искомый вектор должен иметь длину 15. Следовательно, = ´ . Находим
´ = = 75 i – 30 j – 210 k, (5, –2,–14).
Очевидно, что вектор = – тоже удовлетворяет условиям задачи.
Ответ: (5, –2,–14), (–5, 2,14).
8. Даны координаты вершин треугольной пирамиды SABC: A (4, 0, 1), B (5,–1, 1), C (4, 7,–5), S (7, 5, 2). Найти объем пирамиды, площадь основания ABC и высоту (с помощью векторного и смешанного произведений). Найти угол Ð BAC. Укажите, какой вектор перпендикулярен основанию. Изобразите данную пирамиду в декартовой системе координат.
Решение.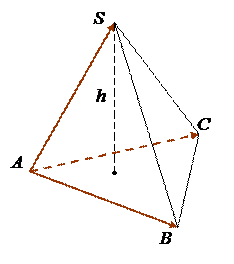 
Находим координаты трех векторов, лежащих на ребрах пирамиды и исходящих из одной вершины:
(1,–1, 0), (0, 7,– 6), (3, 5, 1).
Модуль смешанного произведения этих векторов равен объему параллелепипеда, построенного на этих векторах. Объем же пирамиды составляет 1/6 от объема параллелепипеда: V = ½½.
Смешанное произведение можно вычислить так:
=
Но, поскольку для вычисления площади основания нам понадобится векторное произведение ´, то намного проще воспользоваться определением смешанного произведения: =(´)· . При этом, вероятность арифметической ошибки будет намного меньше. Рекомендуем для проверки правильности вычислений использовать оба способа.
´ = = 
i – 
j + 
k = 6 i + 6 j + 7 k.
S Δ ABC = ½´½= = .
(´)· = 6×3 + 6×5 + 7×1 = 55. V = ½(´)·½= .
C другой стороны, V = SΔ ABC · h . Отсюда h = = = 5.
Согласно определению векторного произведения вектор ´ перпендикулярен и. Поэтому вектор = ´ будет перпендикулярен основанию пирамиды; (6, 6, 7). Угол Ð BAC ищется так же, как и в задаче 5.
Построим изображение данной пирамиды в декартовой системе координат Оxyz.
 |
Ответ: V = , S Δ ABC = , h = 5, (6, 6, 7).
9. Вычислить площадь треугольника ABC, если вершина A находится в полюсе, а две другие имеют заданные полярные координаты: B (6, ), C (4, ). Найти длину BC. Изобразить данный треугольник.
Решение. Нарисуем чертеж к задаче, построив точки B и C по их полярным координатам. Из чертежа и геометрического смысла полярных координат находим, что
Ð BAC = j1– j2 = – = ,
AB = 6, AC = 4.
Тогда
SΔ ABC = AB × AC ×sinÐ BAC = ×6×4×sin = 12× = 6.
По теореме косинусов
BC 2= AB 2 + AC 2 – 2× AB × AC ×cosÐ BAC = 36 + 16 – 2×6×4×(– ) = 76.
Ответ: S Δ ABC = 6, BC = = 2.
10. Новая декартова СК получена из старой переносом начала в точку O ¢(2,–1) и поворотом на угол a = arccos .
а) Выпишите формулы, выражающие новые координаты через старые. Найдите новые координаты точки A, если известны её старые координаты: A (6, 2).
б) Выпишите формулы, выражающие старые координаты через новые. Найдите старые координаты точки B, если известны её новые координаты: B (5, 5).
Решение. а) Новые координаты выражаются через старые по формулам
x ¢= (x – a) × cos a + (y – b) × sin a,
y ¢= –(x – a) × sin a + (y – b) × cos a,
где (a, b) – координаты точки O ¢, a – угол поворота координатных осей. Зная cos a находим sin a и подставляем в формулы:
x ¢= (x – 2) + (y + 1),
y ¢= – (x – 2) + (y + 1).
Для точки A (6, 2) Oxy находим x ¢= 5, y ¢= 0. Значит A (5, 0) O ¢ x ¢ y ¢.
б) Старые координаты выражаются через новые по формулам
x = x ¢ × cos a – y ¢ × sin a + a,
y = x ¢ × sin a + y ¢ × cos a + b.
В нашем случае
x = x ¢ – y ¢ + 2,
y = x ¢ + y ¢ – 1.
Подставляя сюда координаты точки B (5, 5) O ¢ x ¢ y ¢ находим B (3, 6) Oxy.
Ответ: A (5, 0) O ¢ x ¢ y ¢, B (3, 6) Oxy .
