Координаты вектора и точки на плоскости

Пусть на плоскости заданы два неколлинеарных вектора, и произвольная точка O. Пару B = {, } назовем базисом, а тройку R = { O,, } – аффинным репером. Пусть – произвольный вектор. Отложим все векторы из точки O:

= , = , = .

Проведем прямые l ₁= OA , l ₂ = OB. Построим параллелограмм, две стороны которого лежат на прямых l ₁, l ₂, так чтобы C являлась его вершиной. Пусть A ₁ и B ₁ – вершины параллелограмма, лежащие на l ₁ и l ₂ соответственно. Пусть = , = . Тогда по правилу параллелограмма = + . Поскольку ||, а ||, то существуют такие числа x ₁, x ₂, что = x ₁ , = x ₂ Þ

= x ₁ + x ₂. (4)

Это выражение называется разложением векторапо базису B = {, }. Числа x ₁, x ₂ называются координатами вектора в данном базисе. Они же называются координатами точки C относительно репера R = { O, , }. Пишем (x ₁, x ₂) _B, C (x ₁, x ₂) _R. Если заранее известно, о каком базисе или репере идет речь, то их обозначение к координатам не добавляют. Репером на плоскости также называют тройку точек { O, A, B }.

Точка O называется началом координат. Прямые l ₁, l ₂ вместе с выбранными на них направленными отрезками , называются координатными осями. А совокупность координатных осей и начала координат называется аффинной системой координат (СК) на плоскости. Иногда репером называют также тройку точек { O, A, B }, не лежащих на одной прямой.

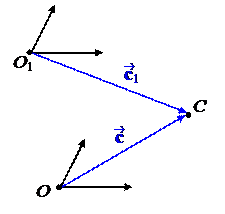Вектор называется радиус-вектором точки C в данной СК или в данном репере. Если мы выберем другое начало координат O ₁, то та же самая точка C будет задаваться другим радиус-вектором = . Поэтому ее координаты изменятся. Координаты же вектора не зависят от выбора начала координат.

Действительно, пусть мы имеем еще одно разложение:

= y ₁ + y ₂, (4¢)

где, например, x ₂ ≠ y ₂ . Вычтем (4¢) из (4):

= (x ₁ – y ₁) + (x ₂ – y ₂) Þ = .

Мы получили, что ||, но мы с самого начала предполагали, что векторы и неколлинеарны. Противоречие. Значит, x ₂ = y ₂. Аналогично доказывается, что x ₁ = y ₁.

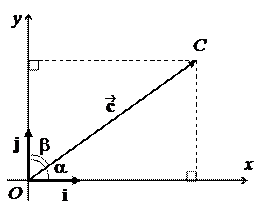Определение. Базис B и репер R называются ортонормированными, если базисные векторы являются единичными и взаимно перпендикулярными (| |= | |=1 и · = 0). В этом случае СК тоже называется ортонормированной. Если, к тому же, пара (, ) является правой, то СК называется декартовой.

Тогда приняты следующие обозначения: координаты (x, y), координатные оси – Ox, Oy, базисные векторы – i , j, направленные отрезки на осях – OE ₁, OE ₂. Векторы i, j называются базисными ортами.

Пусть произвольный вектор в декартовой СК имеет координаты (x, y), т.е. = x i + y j. Домножим это равенство скалярно на вектор i:

· i = x (i · i) + y (j · j) = x ·1 + y · 0 = x.

А, с другой стороны,

· i = ½½½ i ½ cosÐ(, i) =½½ cosÐ(i, ) = P _Ox.

Значит, x = P _Ox . Аналогично получаем y = P _Oy. Таким образом, в декартовой СК координаты вектора совпадают с его скалярными проекциями на координатные оси.

Пусть a =Ð( i, ), b =Ð(j, ). Тогда величины cos a и cos b называются направляющими косинусами вектора .

Пусть в произвольной аффинной СК, которая задаётся репером R = { O, , } известны координаты двух векторов: (x ₁, x ₂), (y ₁, y ₂). Тогда

+ = (x ₁ + x ₂ ) + (y ₁ + y ₂ ) = (x ₁+ y ₁) + (x ₂+ y ₂).

l = l(x ₁ + x ₂ ) = (l x ₁) + (l x ₂).

Значит, вектор + имеет координаты (x ₁+ y ₁, x ₂ + y ₂), а вектор l имеет координаты (l x ₁,l x ₂). Таким образом, при сложении векторов их координаты складываются, а при умножении вектора на число его координаты умножаются на это число. Также легко убедиться, что при вычитании векторов их координаты вычитаются.

Допустим, нам известны координаты двух точек P (x ₁, x ₂), Q (y ₁, y ₂), а = . Выясним, как найти координаты этого вектора.

Пусть = , = . Согласно определению, координаты точки совпадают с координатами ее радиус-вектора. Значит, (x ₁, x ₂), (y ₁, y ₂). По правилу тре-угольника + = , т.е. = – .

Значит, (y ₁– x ₁, y ₂ – x ₂).

Таким образом, для того, чтобы найти координаты вектора надо от координат его конца вычесть координаты начала.